Crain's Petrophysical Handbook - LITHOLOGY / MINERALOGY FROM PE DENSITY NEUTRON (UMA) MODEL

WELCOME TO
CRAIN'S PETROPHYSICAL HANDBOOK

Please be fair to the author. Pay your Shareware fee HERE, and receive the CD-ROM at no extra cost.

LITHOLOGY / MINERALOGY FROM PE DENSITY NEUTRON (UMA) MODEL

Calculating Uma Lithology from PE-Density-Neutron Matrix Parameters

Lithology from PE-Density-Neutron Logs
When the density neutron log is recorded with a photo electric curve, it is often called a litho-density log. Most density neutron logs run today are of this type. The photo electric effect (PE) log curve is sometimes used directly for determining lithology, because it has very definitive matrix values, and linear interpolation between two end points works quite well. However there is a small porosity effect, so a quantity called the photoelectric absorption coefficient (U) is used instead:
       1: U = PE * DENS

The response equation for the absorption coefficient (U) is:
      2: U = UMA * (1 - PHIe - Vsh)
             + UW * PHIe * Sxo
             + UH * PHIe * (1 - Sxo)
             + USH * Vsh

A common assumption is that UH and UW are very small, and that the shale term can be lumped into the matrix term. Thu equation 1 is sometimes used directly. Equation 6 below is more accurate in shaly zones.:

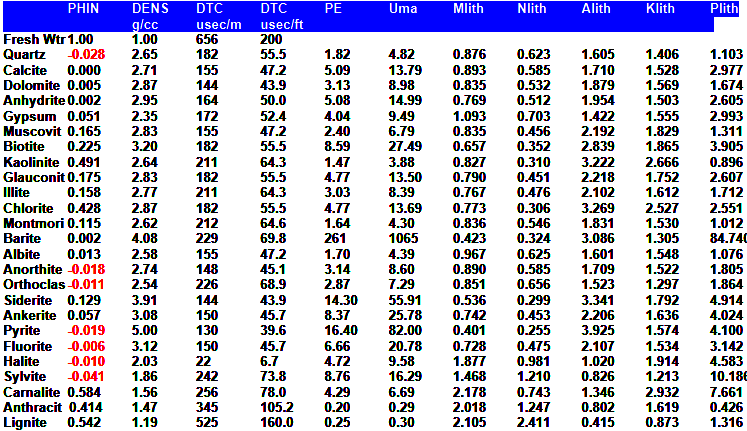
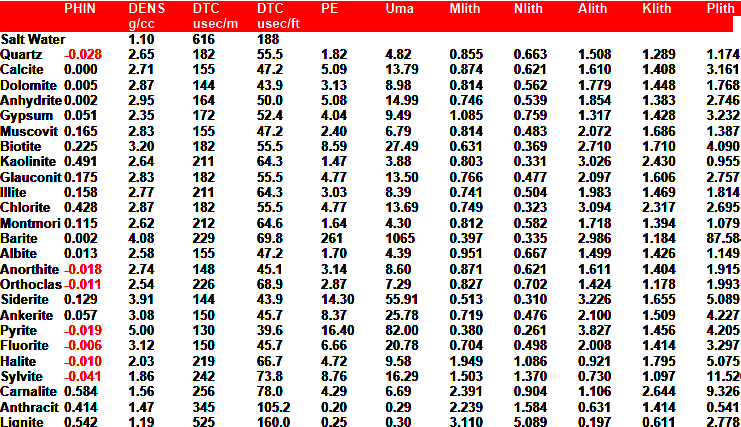
WHERE:
PHIe = effective porosity (fractional)
U = photoelectric absorption cross section (barns/cm3)
UH = photoelectric absorption of hydrocarbon (barns/cm3)
UMA = photoelectric absorption of matrix rock (barns/cm3)
USH = photoelectric absorption of shale (barns/cm3)
UW = photoelectric absorption of water (barns/cm3)
Vsh = volume of shale (fractional)

Note - 1 barn = 1*10^- 24 square centimeters - pretty small cows!

Uma - Apparent Matrix Photoelectric Cross-section
3: DENSSH = PHIDSH * KD1 + (1 - PHIDSH) * KD2

4: USH = PESH * DENSSH
5: DENS = PHID * KD1 + (1 - PHID) * KD2

6: Uma = (PE * DENS - Vsh * USH) / (1 - PHIe - Vsh)

WHERE:
DENS = density log reading (gm/cc)
DENSSH = density log reading in 100% shale (gm/cc)
PE = photoelectric cross section (barns/cm3)
PESH = photoelectric cross section in 100% shale (barns/cm3)
PHIe = effective porosity (fractional)
U = photoelectric absorption cross section (barns/cm3)
UH = photoelectric absorption of hydrocarbon (barns/cm3)
Uma = computed matrix photoelectric absorption cross section (barns/cm3)
USH = photoelectric absorption of shale (barns/cm3)
UW = photoelectric absorption of water (barns/cm3)
Vsh = volume of shale (fractional)

COMMENTS
The Uma values can be used in crossplots with matrix density (DENSma), to determine lithology fractions in a two or three mineral model.

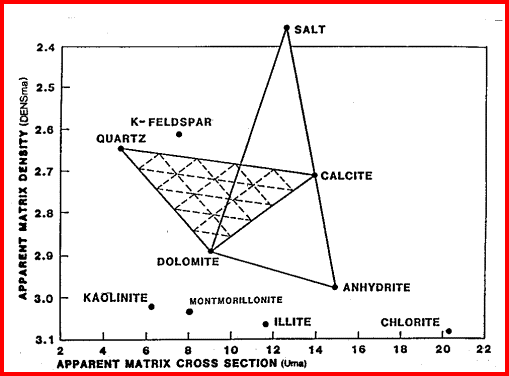
Matrix Density vs Matrix Cross Section Crossplot for Lithology

VROCKpedn - Rock Volume from PE Density Neutron Models
The PE values can be linearly interpolated between any two assumed end points of a two mineral model in the usual way.
7: Min1 = (PE - PE2 - Vsh * PESH) / (PE1 - PE2)
8: Min2 = 1.00 - Min1

This is the ONLY lithology model that works in gas zones, since PE is not affected by gas. All methods that use density, neutron or sonic are invalid in gas zones.

The Uma values can also be linearly interpolated between any two assumed end points of a two mineral model in the usual way.
9: Min1 = (Uma - UMA2 - Vsh * USH) / (UMA1 - UMA2)
10: Min2 = 1.00 - Min1

DENSma and Uma values can be linearly triangulated between any three assumed end points of a three mineral model in the usual way.
      11: D = (Uma * (DENS2 - DENS1) + DENSma * (UMA1 - UMA2)
             + UMA2 * DENS1 - UMA1 * DENS2) / (UMA1 * (DENS3 - DENS2)
             + UMA2 * (DENS1 - DENS3) + UMA3 * (DENS2-DENS1))
      12: E = (D * (DENS3 - DENS1) - DENSma + DENS1) / (DENS1 - DENS2)
      13: Min1 = MAX(0, 1 - D - E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      14: Min2 = MAX(0, E) / (MAX(0, 1 - D - E) + MAX(0, D) + MAX(0, E))
      15: Min3 = (1 - Min1 - Min2)

WHERE:
PHIe = effective porosity from any method (fractional)
PE = measured PE log value of rock mixture
PE1 = PE of first mineral (fractional)
PE2 = PE of second mineral (fractional)
Min1 = relative volume of first mineral (fractional)
Min2 = relative volume of second mineral (fractional)
Min3 = relative volume of third mineral (fractional)
Vsh = volume of shale (fractional)
Uma = computed UMA value of rock mixture
UMA1 = UMA of first mineral (fractional)
UMA2 = UMA of second mineral (fractional)
UMA3 = UMA of third mineral (fractional)
DENSma = computed matrix density value of rock mixture
DENS1 = matrix density of first mineral (fractional)
DENS2 = matrix density of second mineral (fractional)
DENS3 = matrix density of third mineral (fractional)

COMMENTS:
The relative Vmin values must be multiplied by Vrock to get absolute values of V1, V2, V3. Vrock = 1- PHIe -Vsh..

NUMERICAL EXAMPLE:
1. Assume data as follows:
PE = 1.68 barns/cm3
DENS = 2.20 gm/cc
PHIN = 0.27
U = 1.68 * 2.20 = 3.69
Uma = 1.68 * 2.20 / (1 - 0.27) = 5.20

Both PE and Uma are close to the quartz values. If it is dolomitic sandstone, assume:
Vsh = 0.10
PHIe = 0.24
Uqrtz = 4.79
Udolo = 9.00

Min1 = (5.20 - 9.00) / (4.79 - 9.00) = 0.90
Mun2 = 1.00 - 0.90 = 0.10

Vrock = 1 - 0.10 - 0.24 = 0.66.
Vmin1 = 0.90 * 0.66 = 0.60
Vmin2 = 0.10 * 0.66 = 0.06

The rock matrix is 90% quartz, 10% dolomite, but 34% of this is made up of porosity and shale, so the actual volumes of matrix rock are reduced by this amount.

MATRIX ROCK PARAMETERS

	PHIN	DENS	DTC	DTC	PE	Uma	Mlith	Nlith	Alith	Klith	Plith   
		g/cc	usec/m	usec/ft						  	          
Salt Wtr	1.050	1.10	616	188							
Fresh Wtr	1.000	1.00	656	200							
Quartz    	-0.028	2.65	182	55.5	1.82	4.82	0.876	0.623	1.605	1.406	1.103
Calcite	0.000	2.71	155	47.2	5.09	13.79	0.893	0.585	1.710	1.528	2.977
Dolomite	0.005	2.87	144	43.9	3.13	8.98	0.835	0.532	1.879	1.569	1.674
Anhydrite	0.002	2.95	164	50.0	5.08	14.99	0.769	0.512	1.954	1.503	2.605
Gypsum	0.051	2.35	172	52.4	4.04	9.49	1.093	0.703	1.422	1.555	2.993
Muscovite	0.165	2.83	155	47.2	2.40	6.79	0.835	0.456	2.192	1.829	1.311
Biotite	0.225	3.20	182	55.5	8.59	27.49	0.657	0.352	2.839	1.865	3.905
Kaolinite	0.491	2.64	211	64.3	1.47	3.88	0.827	0.310	3.222	2.666	0.896
Glauconit	0.175	2.83	182	55.5	4.77	13.50	0.790	0.451	2.218	1.752	2.607
Illite	0.158	2.77	211	64.3	3.03	8.39	0.767	0.476	2.102	1.612	1.712
Chlorite	0.428	2.87	182	55.5	4.77	13.69	0.773	0.306	3.269	2.527	2.551
Montmori	0.115	2.62	212	64.6	1.64	4.30	0.836	0.546	1.831	1.530	1.012
Barite      	0.002	4.08	229	69.8	 261	1065	0.423	0.324	3.086	1.305	84.74
Albite	0.013	2.58	155	47.2	1.70	4.39	0.967	0.625	1.601	1.548	1.076
Anorthite	-0.018	2.74	148	45.1	3.14	8.60	0.890	0.585	1.709	1.522	1.805
Orthoclas	-0.011	2.54	226	68.9	2.87	7.29	0.851	0.656	1.523	1.297	1.864
Siderite	0.129	3.91	144	43.9	14.30	55.91	0.536	0.299	3.341	1.792	4.914
Ankerite	0.057	3.08	150	45.7	8.37	25.78	0.742	0.453	2.206	1.636	4.024
Pyrite	-0.019	5.00	130	39.6	16.40	82.00	0.401	0.255	3.925	1.574	4.100
Fluorite	-0.006	3.12	150	45.7	6.66	20.78	0.728	0.475	2.107	1.534	3.142
Halite	-0.010	2.03	219	66.7	4.72	9.58	1.877	0.981	1.020	1.914	4.583
Sylvite     	-0.041	1.86	242	73.8	8.76	16.29	1.468	1.210	0.826	1.213	10.18
Carnalite	0.584	1.56	256	78.0	4.29	6.69	2.178	0.743	1.346	2.932	7.661
Anthracit  0.414	1.47	345	105.2	0.20	0.29	2.018	1.247	0.802	1.619	0.426
Lignite	0.542	1.19	525	160.0	0.25	0.30	2.105	2.411	0.415	0.873	1.316

* Multiply DENS (g/cc) by 1000 to get Kg/m3 where needed