|
 CALCULATING
Lithology By Statistical Models
CALCULATING
Lithology By Statistical Models
Determination of
mineral rock composition is an important intermediate task of
formation evaluation. In early days of well log analysis, only
porosity, water saturation and sometimes permeability were
calculated from the logs. Later on, significance of solid rock
component distribution was recognized; while introduction of new
well logging instruments enabled the more accurate assessment of
lithology.
The goal of lithology interpretation is to divide the bulk rock
volume into effective porosity and solid mineral components. The
number of rock components involved in the analysis is dependent on
the quality and quantity of available well logs. As a principle, the
number of components can't exceed the number of input well logs plus
one.
In a well of a carbonate reservoir where a rich set of well logs was
measured, the following components may be determined:
•
Effective porosity
•
Calcite
•
Dolomite
•
Clay
minerals (kaolinite, illite, chlorite etc.)
•
Silt
•
Ferroan minerals (oxides, hydroxides etc.).
In an older well of the same field with only a basic suite of well
logs a three component model is applied:
•
Effective porosity
•
Carbonate (comprising calcite and dolomite)
•
Shale (comprising clays, silt, ferroan minerals).
 Rock Models
Rock Models
In typical
circumstances, the number of rock components present in the
formation exceeds the number which can be reliably determined. (It
is typically not more than five, while in complex lithology the
total number of applied mineral constituents may reach 15 or 20.)
In the case of a
full log suite, the following models could be applied:
•
Porosity, calcite, dolomite, silt, kaolinite
•
Porosity, calcite, dolomite, silt, illite
•
Porosity, calcite, dolomite, kaolinite, Fe-minerals
•
Porosity, calcite, dolomite, illite, Fe-minerals.
It means that, for example, in a rock model either kaolinite or
illite is present, but not both. It is a simplification, which is
necessary to avoid unreliable solutions.
 Response Functions of Well Log Measurements
Response Functions of Well Log Measurements
A great number of
well logs are measured in recent wells. For the task of lithology
determination, only those are involved which are sensitive for the
mineral composition but are not sensitive for other conditions such
as fluid saturations. The mathematical relationships connecting the
rock composition to the well log measurements are called response
functions.
Some typical examples:
Bulk density:
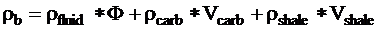
Potassium content:
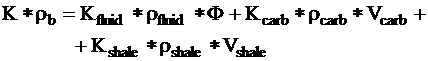
Acoustic (Raymer equation):
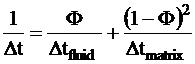
where
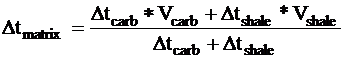
Remarks:
(1)
Some
well log measurements are related to the mass fractions of the rock
components rather than to the volume fractions. In their response
functions, volume fractions are multiplied by the specific density
of the component. Further examples are: gamma ray, photoelectric
effect, Thorium content.
(2)
Response functions may or may not be linear; example of the latter
is the Raymer equation of acoustic sonic travel time. Similar is the
case of SP (spontaneous potential). It means that the software
should be prepared for the handling of systems of nonlinear
equations.
 Zone Parameters
Zone Parameters
It can be observed
in the examples of response functions that some parameters other
than the volume fractions of minerals are involved. They are
generally the specific values of the measured quantity for the rock
component, e.g. the specific density. These are supposed to be known
before the evaluation. They are called "zone parameters"
because their value is constant over a depth interval which covers
(roughly) a geological formation.
Sources of information for zone parameters are the following:
•
In
publications of well logging companies, handbooks etc. these
parameters are published as glossary data; e.g. specific density of
different minerals is well known from the literature.
•
The
study of the measured well logs themselves (in the form of hard
copies, crossplots etc.) can reveal some parameters. E.g. layers
where shale content is near to 100 % can suggest the zone parameters
of the "shale" rock component.
•
Log
analysis can be calibrated to cores if they exist. In general,
geological descriptions based on cores and drill cuttings reveal the
minerals existing in the formation. Comparison of core porosity
measurements with porosities computed from well logs may indicate
that zone parameters of the "porosity logs" (density, neutron,
sonic) are not correct.
•
In
field-wide studies where several wells are measured in roughly the
same period by the same logging company, experience from
interpretation of one well can be transferred to another well
regarding selection of rock components, rock models, zone parameters
etc.
•
There is a feedback between zone parameters and the analysis. If
there is a systematic difference between measured values and
theoretical response values of a well log, it may be reduced by
modifying zone parameters.
 Zones of ANALYSIs
Zones of ANALYSIs
Quantitative
analysis of lithology in a well is carried out in a depth interval
which is important regarding the hydrocarbon production; that is
generally the potential reservoir interval and some adjacent
intervals. It may be homogeneous in respect of lithology, but often
it covers more than one geological formations which are distinctive
in age, mineral composition etc. Rock components, rock models and
zone parameters should be set up differently in these formations.
The basic zonation of the interpreted interval is controlled by the
geological zonation in terms of rock formations.
Necessity of introducing different zones of interpretation may also
emerge because of technical reasons. In some part of an interpreted
formation quality and existence of well logging measurements may
differ. For instance, some of the input well logs may be useless
because of large rugosity effects. In that interval reduction of
input information means reduction of the richness of outputs, e.g.
less detailed rock models can be applied. This is done in the
software by declaring the rugous interval as a different zone.
In the lithology part of the software, zones of interpretation are
defined by listing the depth intervals belonging to that zone. For
each rock component (mineral) and rock model, the list of zones
where that particular rock component or model is applied should be
declared. We can apply the same mineral in different zones with
different zone parameters. In that case in output results the
mineral can be displayed as the same in different zones, but during
computation in each zone it is evaluated with its particular
parameters in that zone.
 Deterministic analysis
Deterministic analysis
In deterministic
systems of interpretation the number of unknown volumetric fractions
equals the number of equations (including the log response equations
and the material balance equation). Validity of the result should be
checked, e.g. the equations can yield negative volume fractions
which should be avoided .
There are two approaches to this interpretation: sequential and
simultaneous.
Deterministic
interpretation in a sequential way
is the traditional
(conventional) way of lithology determination. The volume fraction
of one component is determined from one well log. (The response
function of that well log is simplified so that only the volume
fraction of that component is involved as the unknown quantity.) The
second component is determined from another well log measurement; in
its response function the volume fraction of the first component may
be already involved. In a similar way at each step a new component
is determined by using the response function of a well log
measurement and volume fractions of components computed in previous
steps. The last component is computed from the material balance
equation.
A good example is determining the lithology of a shaly sandstone
formation from gamma ray and neutron. In the first step, shale
volume is computed from the formula
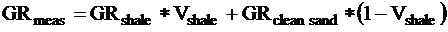
In the second step (where Vshale is already known) porosity is
computed from the neutron porosity measurement:
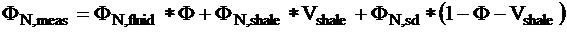
In the last step the material balance equation yields the volume
fraction of sand:
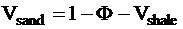
Solving an actual interpretation task may be more complicated than
this simple procedure. First, some constraints should applied, e.g.
neither volume fraction can take negative values. Secondly, a
branching can occur: different shale parameters can be applied if
the points representing the depth sites separate into groups on a
crossplot; in our case, on the crossplot of neutron porosity vs.
gamma ray. (This corresponds to the application of different rock
models in the statistical interpretation.)
Deterministic
interpretation by solving a system of equations is an alternate to
sequential methods.
The response functions (plus the material balance equation) can be
treated as a system of equations with the volume fractions of rock
components as unknowns. This system of equations can be solved by
appropriate mathematical methods. Advantages of this approach are:
•
All
unknown volume fractions are computed simultaneously, so the
complete forms of response functions are used (e.g. in the previous
example effect of porosity on gamma ray measurement is not ignored).
•
Handling of constraints on the accepted range of volume fractions is
more consistent. For example substituting zero values for negative
volume fractions will lead us to more equations as unknowns so it
leads us to the statistical interpretation.
•
Cumulative addition of errors associated to the sequential way is
reduced.
 Statistical AnALYSIS
Statistical AnALYSIS
In the
deterministic algorithms, the number of equations (with material
balance) equals the number of unknown rock components. In
statistical interpretation the number of equations exceeds the
number of unknowns. It means that the number of well log
measurements is at least as large as the number of rock components
but generally larger. It means that the system is mathematically
over-determined: no exact solution exists which satisfies all the
equations.
The following method is applied for solving the task of statistical
interpretation:
•
A
measure of quality called incoherence is defined for the evaluation
of each approximate solution for the system of equation;
•
A
mathematical optimization problem is defined: find the set of volume
fractions which gives the optimum value of the incoherence;
•
Constraints on the solution (upper and lower bounds on the volume
fractions) are treated by including penalty terms in the quality
indicator if the constraints are violated.
•
Advanced methods of mathematics are applied for the solution of the
optimization problem; it yields a set of volume fractions of
minerals as well as the value of incoherence.
The quality indicator is constructed by examining the reliability of
each well log measurement involved. An error term is associated to
each well log and the evaluation of each measurement by means of
response function. The sources of error are the following:
•
Environmental effects: borehole enlargement and rugosity,
interaction with drilling mud etc.;
•
Errors in the principle of measurement (statistical nature of
radioactive radiation);
•
Errors in depth matching and effects in difference of depth of
investigation of the different well logging instruments;
•
Further on, the selection of rock models and zone parameters is
burdened with errors.
All these diverse sources of error are added together and result in
a random error for which we can assume a normal distribution with
zero mean value and a standard deviation of si for the
i-th measurement and answer.
The quality indicator, incoherence, is defined by the formula:
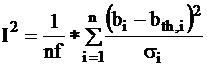
where
bi:
measured value of the i-th well log;
bth,i:
value computed from the response function of the i-th well log,
called answer;
si:
standard deviation of error for the i-th measurement.
nf:
degree or number of freedom which equals:
number of well
logs + 1 - number of unknowns
In a simple rock
development, it is sufficient to apply a single rock model like the
three-component sandstone model of porosity, sand (quartz) and
shale. In real situations further minerals or other lithology
components accumulate in the rock such as calcite, silt, clays,
ferroan minerals etc. All of these components ought to be included
in the interpretation, but their number would exceed the number of
well log measurements. In that case multiple rock models are
defined; in each of them the number of equations is greater than the
number of components.
The statistical over-determined nature of the interpretation provides
the quality indicator, incoherence, which enables us to select
between the competing rock models. As a general principle, the rock
model with the smallest incoherence is accepted as valid at each
depth site. However, the software enables the overruling of this
automatic model selection. The following reasons may verify the
change of the least incoherence model:
•
The
creation of longer homogeneous intervals requires the comparison of
model selection for neighbouring depth sites and change of models if
another model with only slightly larger incoherence fits better into
the environment, according to the principle of geological
consistency.
•
If
the lithologic rock composition provided by the selected model
contradicts our knowledge from other sources of information (e.g.
cores), a more plausible model can be accepted.
Generally the interpretation is carried out in cycles: there is an
initial selection of minerals, rock models and zone parameters. Then
the interpretation is carried out and the results are examined.
Occurrence of unexpectedly high incoherences indicates that the
input of interpretation should be changed:
•
New
minerals (rock components) should be included;
•
Further rock models should be applied;
•
Zone
parameters should be modified.
 Statistical Method DETAILS
Statistical Method DETAILS
Well log measurements
Suppose L1,
L2, ? Lm
are well log measurements made in a borehole. A depth interval is
selected where lithology should be evaluated: volumetric fractions
of rock components (including porosity and solid minerals) should be
determined. The interval is divided into zones (Z1,
?Zn) which are constructed of
one or more sub-intervals. The Li
log measurements are available at regular frequency - usually at
each half foot.
The set of well log measurements involved in lithology determination
can be changed in different zones. (E.g. gamma ray is involved in a
shaly sandstone formation but it is abandoned in a shale-free
carbonate zone.) It is assumed that all well log measurements are
available in the zones where they are applied.
Rock components and models
The bulk rock
volume is divided into effective porosity and solid rock components.
The solid components may be minerals (calcite, quartz, kaolinite
etc.) associations of minerals (ferroan minerals: oxides and
hydroxides) or lithology types (limestone, sandstone, shale). Each
rock component is characterized by its specific value of the applied
rock measurements (zone parameters).
For each rock component its scope (i.e. the list of zones where it
is applied) should be listed. A mineral can be present in one zone
only or in several zones. In the latter case, its zone parameters
may or may not be the same in different zones.
The number of mineral components present in a formation generally
exceeds the number of rock components which can be reliably
determined by the statistically over-determined interpretation
technique.
Several subsets of rock components occurring together are defined
and called rock models. For each model, the zones where it is
applied should be listed.
Response functions and zone
parameters
Response functions
are mathematical relationships between the logging parameters and
the rock mineral composition. These are theoretical functions which
don't account for random errors or factors not involved in the
model. Actual log measurements and theoretical responses generally
differ.
The zone parameters are specific parameters of response functions
which are constant for all depth sites in a zone of interpretation.
Generally one zone parameter reflects the effect of a rock component
in each response function.
System of equations
The set of
response functions creates a system of equations together with the
material balance equation; the latter describes the fact that the
sum of all volume fractions in a unit volume equals one:
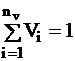
It is included in the system of equations where it has a special
status: while response functions are considered as approximations
burdened with errors, the material balance equation is exact.
A system of equations is set up where the number of unknown rock
volume fractions is smaller than the number of equations. The
statistical over-determined nature of the method is characterized by
the degree of freedom:
nf
= nl + 1 - nv
Incoherence
Normalized
incoherence is defined in Section 7. If the deviation of the
measured logs and the theoretical responses is considered as a
random error variable, the value of nf *.I2 has a
chi-square distribution.
Normalized incoherence as measurement of quality of interpretation
is used to the following purposes:
·
At
each depth site with each model, the set of volume fractions which
minimizes incoherence is accepted as the solution.
·
At
each depth site where multiple models are applied, the model with
the least incoherence is selected (if other considerations don't
override it).
·
Statistical characteristics of incoherence in a well or in a zone
are used as a general indicator of quality of interpretation.
Improvement by changing selection of minerals, values of zone
parameters, etc. is justified by the decrease of incoherence.
 Mathematical Solution
Mathematical Solution
The mathematical
problem that is to be solved for each model at each depth site is
the following:
·
There is a system of equations consisting of nl
+ 1 equations and nv unknowns
where nv < nl + 1 . The overdetermined nature of the system (more
equations than unknowns) means that an exact mathematical solution
generally is not found.
·
An
object function (the normalized incoherence) is set up which
describes the quality of each approximate solution of the system of
equations. The goal is to find the set of volume fractions which
minimizes the incoherence.
·
The
restrictions on the valid range of volume fractions are taken into
account. Penalty terms are added to the object function which assure
that the final solution is inside the accepted range.
An iterative method is applied starting from an arbitrary initial
approximation. A variant of the Newton method is applied which
rapidly converges to the minimum place of the object function. (It
is a local approximation of the function by a quadratic function at
each step.)
 Presentation of Results
Presentation of Results
Strip logs of
lithological composition are the usual way of graphical presentation
of the interpretation. The volumetric fractions of the different
rock components are displayed versus depth. At each depth site, the
area covered by the specific colour code of the rock component is
proportional to the volumetric fraction.
Statistical tables about abundances of rock components (total and
separated by models) are printed together with the tables
representing the rock models and zone parameters.
Although the strip logs of lithology are the most useful for the end
user (geologist, reservoir engineer etc.), other forms of
presentation are also important for the log analyst. The crossplots
of response vs. measurement for the input well logs are crucial for
the evaluation of the quality of interpretation. Clouds of points
moved far away from the identity line may reflect two conditions:
•
The
zone parameters of one (or more) minerals regarding that input log
are not correct and should be modified;
•
Another rock component exists in the formation and it should be
included in the rock models.
Crossplots of two rock components are suitable for investigating the
reservoir quality of the formation. Especially, crossplot of volume
fraction of shale vs. porosity is important in shaly sandstones.
Irregularity of the crossplot (e.g. points with high porosity and
high shale content) may refer to improper shale zone parameters.
Cumulative histogram of squared incoherence is used for the
calibration of the standard errors of input logs so as to
approximate the theoretical chi-square probability distribution.
 Optimization of Zone Parameters
Optimization of Zone Parameters
Rock components
involved in lithology interpretation are different in their degree
of certainty. Some of them are stable minerals (such as quartz,
calcite etc.) with well known attributes regarded as worldwide
constants. Other components are more complex mixtures of minerals
such as shale or ferroan minerals.
Their zone parameters are known only with a higher degree of
uncertainty.
Another source of zone parameter uncertainty is the presence of
systematic errors in well log measurements. Some of these errors can
be eliminated by correction of the measured logs. However, often the
deviation of zone parameters from their expected values is also
necessary. In these cases
adjustment of zone parameters is necessary. Beside manual
improvement, necessity of automatic optimization emerges. The
criterion of optimization is the magnitude of incoherence. Iterative
methods can be applied by modifying the selected set of zone
parameters until the minimum value of the weighted sum of squared
incoherence is reached.
We have to emphasize that automatic zone parameter optimization
should be applied with great care. Only one (or at most two) zone
parameter of a rock component can be altered by this method;
similarly, only a limited number of zone parameters belonging to the
same log response function should be changed. Otherwise, artificial
mathematical objects will be generated instead of real rock
components.
 Role of Standard Errors
Role of Standard Errors
Another set of
parameters which have great influence on lithology interpretation
are the si
standard errors associated with well logs included as input
parameters. Both the magnitude of si-s
relative to each other and their absolute value are important.
Increasing the value of a si
term decreases the influence of the respective well log on the
results of lithology interpretation. The crossplot of response vs.
measurement of that log will show a wider cloud of points with
statistical characteristics of regressional relationship degraded
(the correlation coefficient decreases, closeness of regression
coefficients to 1 and 0 decreases, error of estimation increases).
Decreasing the value of a si
term increases the influence of the respective well log. The
crossplot of response vs. measurement of that log will show a
narrower cloud of points. The correlation coefficient increases,
closeness of regression coefficients to 1 and 0 increases, error of
estimation decreases.
In both cases, influence of other well logs on the interpretation
changes the opposite way, e.g. increasing standard error of one log
(i.e. decreasing influence of that log) will increase the influence
of the other logs. One factor should be considered when evaluating
the regressional relationship of response vs. measurement: the
inherent variability of the measured well log values (reflecting the
variability of the rock in respect of that well log) also affects
the closeness of fit.
No fixed rules exist for the setting of relative magnitudes of
standard errors Si,
however, the following guidelines can be applied:
·
Ratios of standard errors are based on the ratios of measurement
errors (repeat sections can be used for the evaluation of this).
·
The
influence of the well logs should reflect their quality and their
ability to reveal lithology in the formation. (E.g. gamma ray may
have greater influence in shaly sandstones than in carbonates.)
·
Both
extremities (input logs with negligible influence or with
overwhelming influence) should be avoided.
The absolute values of standard errors si
are calibrated by comparing the practical distribution
of squared incoherences to the theoretical chi-square distribution.
In FlexInLog, the upper quartile of the distribution is used as it is
more robust parameter than the average. The si-s
are multiplied with a common factor so that the upper quartile
equals 0.5.In this way
interpretations in different wells become comparable. E.g. depth
sites where I2 > 2 considered as cases of high
incoherence with unreliable lithology interpretation; calibration of
standard errors assures that this criterion is consistent for
different evaluations.
 Reducing Unknowns
Reducing Unknowns
Constraints on the
valid range of rock components are applied in lithology
determination. The trivial conditions of 0 £ Vi
£ 1 should be met, besides, upper limits on some accessory minerals
Vi £ (Vi)max
<< 1 may be applied. The most frequent case of violation is that the
volume fraction of a component tends to be negative; the
mathematical algorithm sets this volume fraction equal to zero.
Theoretically this means that the number of unknowns is reduced and
the degree of freedom nf is
increased by one. The increase of nf
is applied in FlexInLog in the formula of the incoherence; this fact
should be kept in mind when comparing incoherences of evaluations by
models with different numbers of (existing) rock components.
A special case of this phenomenon occurs when deterministic
evaluation is applied. Using a system of equation with nf
= 0, an exact mathematical solution is computed. Generally, none of
the constraints is violated and every equation is satisfied without
error (responses equal measurements for each input well log).
If some constraints of avoiding negative rock components are
violated, these components are substituted with zeroes. This reduces
the number of unknown components and the system of equations is
transformed into an over-determined one (nf > 0). The same
mathematical algorithm can be used as for the statistical
interpretation (standard errors should be defined). Responses are no
longer equal to well log measurements, so incoherence can be
computed and used for the assessment of the quality of
interpretation.
The handling of violations of constraints this way provides some
benefits of statistical interpretation for the deterministic
interpretation. The mathematically optimal (least incoherence)
solution is found if one or more of the volume fractions of rock
components becomes zero.
 Determination of Matrix Density
Determination of Matrix Density
Matrix density is
obtained from the formula:
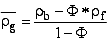
where rb:
the measured (and corrected) log density
F
: effective porosity provided by the quantitative lithological
interpretation
It is important
to compare matrix density obtained from well log analysis with those
measured on cores, since it can reveal some errors of lithological
interpretation; for instance non-existing mineral or lithological
components were taken into account in the applied rock models, what
may cause serious difference between the two compared grain
densities.
|

