|
 Water Saturation in the
Dual Porosity Model
Water Saturation in the
Dual Porosity Model
The average
water saturation of the composite system is calculated using
a statistical parameter, P, originally introduced to the oil
industry by Porter, Pickett, and Whitman. Empirically, it
has been found that P has a normal distribution for
intervals which are 100 per cent saturated with water.
Intervals with some hydrocarbon saturation deviate from the
normal distribution.
|
Calculating
P
For sonic logs:
15a: P = (RESD * (DELT - DELTMA) ^ Md) ^ (1/2)
For density logs:
15b: P = (RESD * (DENS - DENSMA) ^ Md) ^ (1/2)
If effective porosity has been computed from density
neutron crossplot:
15c: P = (RESD * (PHIe ^ Md) ^ (1/2) |
WHERE:
DELT = sonic log reading (usec/ft
or usec/m)
DELTMA = sonic matrix
transit time (usec/ft or usec/m)
DENS = density log reading
(g/cc or kg/m3)
DENSMA = matrix density
(g/cc or kg/m3)
Md = cementation exponent
for double porosity model, found from a Pickett plot
P = statistical parameter
(unitless)
PHIe = effective porosity
of double porosity system (fractional)
RESD = deep resistivity
log reading (ohm-m)
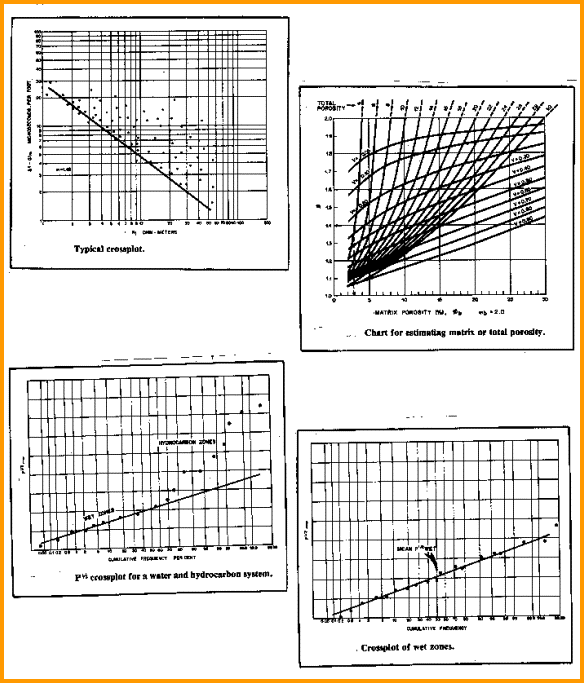
Pickett plot, partition factor, and probability
graphs for Aguilera’s dual porosity model
This
illustration, bottom left, shows a schematic of P vs cumulative frequency
on probability paper for a water and hydrocarbon system. The 100
per cent water saturated zones form a straight line, and the hydrocarbon
intervals deviate from this line and are thus easily recognized.
Bottom right shows the same type of plot for only the
water bearing intervals. The mean value of P for water zone, Pmean,
is determined from this graph at a cumulative frequency of 50
per cent. An arithmetic average of the P values from the water
leg is usually satisfactory, so the probability plot is not necessary.
Having
the mean value of P from the water zone allows us to calculate
the water saturation of the dual porosity system from the
following.
|
Partitioning water saturation
16: Swd = (Pwtr / Phyd) ^ (1/N)
17: Swf = (VISW * WOR) / (Bo * VISO + VISW * WOR)
18: Swe = (Swd - V * Swf) / (1 - V)
|
Where:
Bo = oil formation volume
factor (vol/vol)
N = water saturation
exponent (unitless)
Phyd = parameter P for
each hydrocarbon zone (unitless)
Pwtr = mean value of P for
water bearing intervals (unitless)
Swd = water saturation for
the double porosity system (fractional)
Swe = water saturation for
the matrix rock (fractional)
Swf = water saturation for
the fracture (fractional)
VISW = water viscosity
(cp)
VISO = oil viscosity (cp)
WOR = water/oil ratio, (vol/vol)
This
long evaluation process requires the reading, plotting, and
crossplotting of large volumes of data, and requires a large number
of calculations. This makes it an ideal computer application and
hand calculation is not recommended. A solution for a gas reservoir
was never published. In many cases Swf is assumed to be 0.0 (because
WOR = 0) so this assumption can be used for gas wells also.
NOTE:
This is essentially an "Rwa type" saturation method and relies on
the presence of a water zone. In the absence of a water zone, an
rchie water saturation solution (Swa) will have to suffice, giving
the equivalent of Swe. Swf is not derived from log data. If
parameters are unknown, start with VISW =1.0, VISO = 2.0, WOR = 0.0,
and Bo = 0.8. This makes Swf = 0.0 during production, which is close
to the truth.
|
Standard
Archie solution
19: Swa
= (A * RW@FT / (PHIe ^ Md) / RESD) ^ (1/N) |
Where:
A = tortuosity exponent (unitless)
Md = cementation exponent
for matrix rock with fractures (unitless)
N = saturation exponent (unitless)
PHIe = effective porosity
(fractional)
RESD = deep resistivity
log reading (ohm-m)
RW@FT = water resistivity
at formation temperature (ohm-m)
Swa = effective water
saturation (fractional)
RECOMMENDED
PARAMETERS:
If zone is not heavily fractured:
For sandstones:
A = 0.62
Mb = 2.15
N = 2.00
For
carbonates:
A = 1.00
Mb = 2.00
N = 2.00
If
zone is fractured:
Mb = 1.4 to 2.0
A = 1.00
N = 2.00
NOTE:
The symbol M is used elsewhere in this book as the cementation
exponent for the Archie equation. Mb is used here to indicate
the use of Archie for the fractured reservoir case.
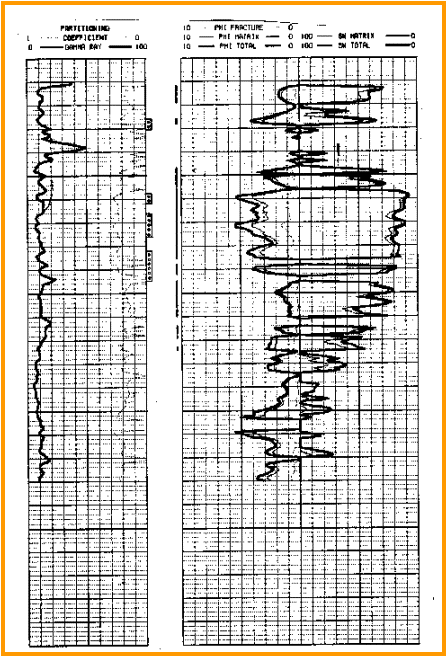
Dual porosity model results in a Williston Basin
well
The
log shows the computed log results for a Williston Basin Mississippian
fractured zone. The contribution of fracture related porosity is about
1% porosity, but water saturation is 5 to 10% lower than the analysis
without the fractures. The partitioning coefficient varies and
was solved by iteration.
|

