|
 Dual Porosity Model
in Fractured Reservoirs
Dual Porosity Model
in Fractured Reservoirs
The first
assumption made is that matrix and fractures are connected
in parallel and 100 per cent saturated with formation water:
|
Recall that we renamed the porosity terms as follpws:
5: PHIe = PHIm + PHIf
6: PHIt
= PHIe + Vsh * BVWSH
Aquilera’s
partitioning concept:
7: V = (PHIe - PHIm) / (PHIe * (1 - PHIm))
|
Since it
is the breakdown of PHIe into PHIm and PHIf that we are seeking,
equation 7 cannot help us find V directly. A useful approximation
is:
|
A practical
partition factor
7a: V = (PHIe - PHIsc) / PHIe
|
This
also assumes that PHIe >= PHIsc and that PHIsc is properly corrected
for lithology and shale.
|
Find Ro and Rfo
8: Ro =
(1 / PHIe^Mb) * RW@FT
9: 1 / Rfo = V * PHIe / RW@FT + (1 - V) / Ro
10: F = Ro / RW@FT
11: Fd = Rfo / RW@FT
Combining
equations:
12: Fd = 1 / (V * PHIe + (1 - V) / F)
13: PHIm = (((PHIe ^ Md) - (V * PHIe)) / (1 - V)) ^ (1/Mb)
14. PHIf = PHIe - PHIm |
Where:
PHIe = effective porosity
of dual porosity system (fractional), usually taken equal to PHIxnd
from density neutron crossplot
PHIm = effective matrix
porosity in dual porosity system (fractional)
PHIf = effective fracture
porosity of dual porosity system (fractional)
PHIsc = sonic porosity
(fractional)
Rfo = composite system
resistivity at 100% Sw (ohm-m)
Ro = primary porosity
resistivity at 100% Sw (ohm-m)
RW@FT = formation water
resistivity at formation temperature (ohm-m)
F = formation factor for
matrix rock (unitless)
Fd = formation factor for
dual porosity model (unitless) Md = cementation exponent for dual
porosity model, found from a Pickett plot
Mb = cementation exponent
for un-fractured matrix rock, found from laboratory measurement, a
Pickett plot in an un-fractured zone, or from assumption based on
lithology
V = partitioning
coefficient (fractional)
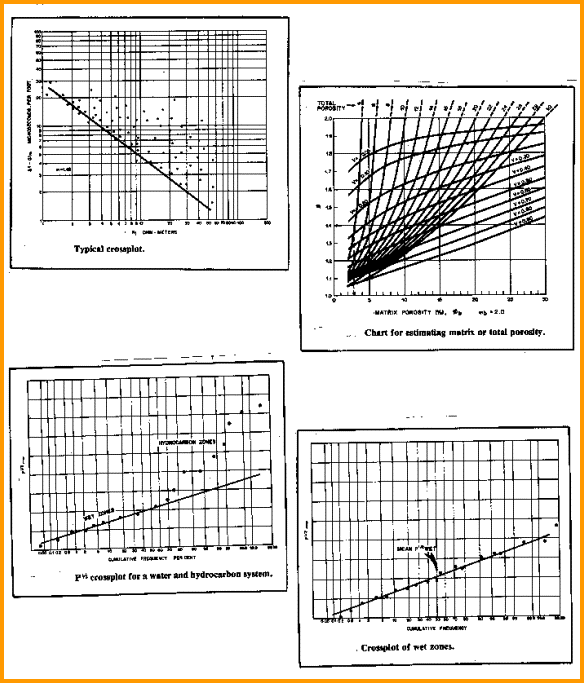
Pickett plot, partition factor, and probability
graphs for Aguilera’s dual porosity model
Top right shows the graphical solution to Equation 5 for
various values of Mb. If, for example, Md is 1.4, Mb = 2.0, and
effective porosity (PHIe) is 0.04, then the partitioning coefficient
V is 0.26; thus, the fracture (-related) porosity (PHIf) is 0.0106
and the matrix porosity (PHIm) is 0.0294.
The
fracture porosity in this example is impossibly high. It must
contain some vuggy or solution (fracture-related) porosity
as well, so this method should be used with caution at all
times.
|
To
compare this result to core analysis, we must find matrix porosity
from logs as a function of the matrix bulk volume (PHIcore),
eliminating the volume of the fractures. Comparing
to core porosity:
99: PHIcore = PHIm / (1 - PHIf)
Where:
PHIcore = effective matrix porosity corrected to match core (fractional)
PHIm = effective matrix porosity in double porosity system (fractional)
PHIf = effective secondary porosity of double porosity system
(fractional)
For
example, if V is 0.26 and PHIe is 0.04, then fracture porosity,
PHIf, is 0.0106 and PHIm is 0.0294 as before, and:
PHIcore = 0.0294 / (1 - 0.0106) = 0.0297
NOTE:
If the partitioning coefficient V cannot be found from sonic versus
density neutron crossplot porosity, then equation 2 and 7 must
be solved iteratively.
Fracture
detection methods usually require that the fractures intersect the borehole
and be invaded by mud of relatively low resistivity. This is not
the case with the method presented here. In some cases it has
been possible to detect fractures located within the radius of
investigation of the logging tools, but not intercepted by the
borehole.
RECOMMENDED
PARAMETERS:
Md is in the range 1.0 to 1.8
Mb is in the range 1.6 to 2.6
V is in the range 0.0 to 0.5
|

