SHALE Volume FROM Gamma Ray LOGS
The two most common shale indicating logs are the gamma ray (GR) and spontaneous potential (SP) logs. The units of measurement for GR are API units or counts per second, and for SP are millivolts.

The resistivity, neutron, and sonic are sometimes used individually, and the separation between density porosity and neutron porosity is also widely used. More rarely, the electromagnetic propagation attenuation curve is available and is an excellent shale indicator, especially in thin bedded (laminated) sand-shale sequences.

There are several flavours of gamma ray logs. The conventional natural gamma ray log is usually abbreviated GR or SGR and is the curve most commonly available. The natural gamma ray spectral log produces the same total gamma ray curve, usually abbreviated SGR. A second gamma ray curve, called CGR, has the gamma rays from uranium filtered off. Thus CGR is always less than or equal to SGR. If a CGR is available, it should be used in preference to the SGR or GR logs.

Gamma Ray Corrected for Borehole Effect
Borehole size, mud weight, tool type, and poor calibration affect the gamma ray response to the rocks. There are two ways to compensate for this. One is to apply explicit borehole corrections to the log curve data, as shown in this Section. Such explicit corrections cannot fix poor calibration or logs in odd units (such as counts per second or micrograms Radium equivalent per ton of rock.  This is covered in the next Section on this page which covers log normalization.

      1: IF DEPTHUNIT$ <> "METRIC"
      2: THEN GRc = GR * (l + 0.04 * (MWT - 8.3)) * (1.0 + 0.06 * (CAL - 8))
      3: IF DEPTHUNIT$ = "METRIC"
      4: THEN GRc = GR * (1 + 0.000322 * (MWT - 1000)) * (1.0 + 0.0024 * (CAL - 203))
      5: IF MWT = Null
      6: OR IF BITZ = Null
      7: OR IF CAL = Null
      8: THEN GRc = GR

Where:
  CAL = caliper log reading (hole size) (in or mm)
  GR = gamma ray log reading (API units)
  GRc = gamma ray log reading corrected for borehole size and mud weight (API units)
  MWT = mud weight (lb/US gal or kg/m3)

COMMENTS:
The fixed constants in these formulae may need to be varied for some logging tools. A chart indicating corrections for more complex situations and the associated mathematical formulae are shown below, courtesy of Dresser Atlas. If mud properties are unknown, the usual solution is to do nothing and use the GR value as is.

RECOMMENDED PARAMETERS:
None. Default value for MWT is usually 10 lb/USgal or 1250kg/m3

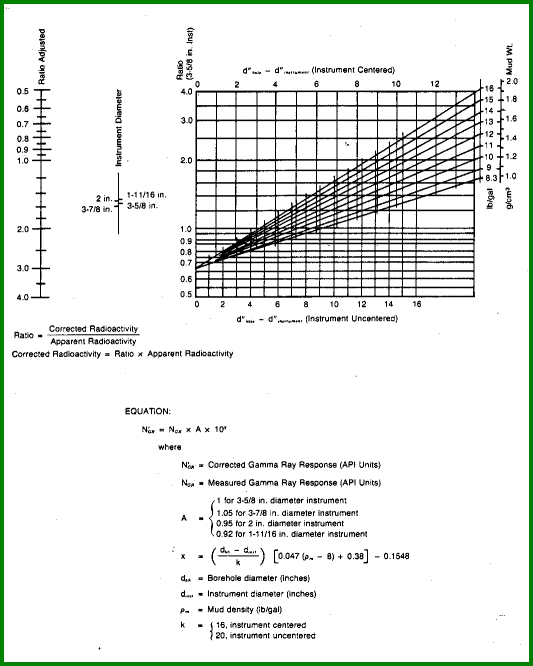
Borehole Corrections for Gamma Ray

Gamma Ray LOG NORMALIZATION
Gamma ray log normalization is based on the concept that all clean sands in an area should have the same GR log reading, and that all pure shales should have the same GR values. The assumption includes the fact that there is a clean sand and a pure shale in each well in the zone of interest (or at least nearby) and that there are no major geological reasons for the values to vary across space. Normalization also helps reduce mud weight and hole size effects, but the explicit corrections are probably best if done first, then normalization applied afterward.

The equation is:
      9: GRn = GRMIN + (GRMAX - GRMIN) * (GRcor - GRLOW) / (GRHIGH - GRLOW)

Where:
  GRn =  normalized gamma ray (API units)
  GRcor = input  gamma ray corrected for borehole and mud weight (any units)
  GRMIN = GR clean sand value to normalize to (API units)
  GRMAX = GR shale value to normalize to (API units)
  GRLOW = GR clean sand value in this well/zone (any units)
  GRHIGH = GR shale value in this well/zone (any units)

CAUTION: Normalization can remove natural geological variations that may have significance in understanding the reservoir variations across space. For example, if calcite cement varies from place to place, normalization will remove porosity trends that vary with cementation. Similarly, on a GR log if feldspar content or clay type varies, this knowledge will be lost.

COMMENTS
This is the method most used for GR and SP curves but can be used with care on any log curve.

NUMERICAL EXAMPLE
Assume you want to re-scale all GR logs so that all clean lines are at 20 API units and all shale lines are at 120 API units. That makes GRMIN = 20 API units, GRMAX = 120 API units for all wells
Assume GRLOW = GR0 = 30 API units, GRHIGH = GR100 = 145 API units in THIS zone in this well.
Assume actual GR at a depth level = 55 API units
   1: GRn = 20 + (120 - 20) * (55 - 30) / (155 - 30) = 40 API units


Shale Volume from the Gamma Ray
The response equation for the gamma ray log follows the classical form:

        10: GR = PHIe * Sxo * GRw (water term)
                    + PHIe * (1 - Sxo) * GRh (hydrocarbon term)
                    + Vsh * GRsh (shale term
                    + (1 - Vsh - PHIe) * Sum (Vi * GRi) (matrix term)

Where:
  GRh = log reading in 100% hydrocarbon
  GRi = log reading in 100% of the ith component of matrix rock
  GR = log reading
  GRsh = log reading in 100% shale
  GRw = log reading in 100% water
  PHIe = effective porosity (fractional)
  Sxo = water saturation in invaded zone (fractional)
  Vi = volume of ith component of matrix rock
  Vsh = volume of shale (fractional)

Both GRw and GRh are zero. GRi is equal to the background radiation in non-shaly rock and is called GR0 in this book. GRsh is the log reading in shale, called GR100 here. The effect of porosity is very small, so that term also is assumed to be zero. The response equation thus reduces to:

      11: GR = Vsh * GR100 + (1 - Vsh) * GR0

When solved for Vsh, this equation becomes:

        12: VSHgr = (GR - GR0) / (GR100 - GR0)
        13:  VSHgr = Min(1, Max(0, VSHgr))

Where:
  GR = gamma ray log reading in zone of interest corrected for borehole size (API units)
  GR0 = gamma ray log reading in l00% clean zone (API units)
  GRl00 = gamma ray log reading in l00% shale (API units)
  VSHgr = shale volume from gamma ray log (fractional)

COMMENTS:
Apply borehole corrections and normalize logs if desired before doing Vsh calculations.

Use CGR, if available, in preference to GR or SGR curves. CGR has uranium effect removed. 

Do not apply borehole corrections to ECGR - that step has already been done at thhe lpgging unit. Read log heading comments to see what was done at the wellsite.

The gamma ray method for shale volume is preferred in the majority of cases. The exceptions are radioactive dolomites and sandstones, and zones which contain feldspar or uranium.

Use of the data from the natural gamma ray spectral log helps to resolve these cases. See following sections.

References:
 1. Gamma Ray Well Logging,
     L.G. Howell, A Forsch, Geophysics, 1939.

 2. Gamma Ray Logging,
     F.P. Kokesh, Oil and Gas Journal, 1951.

 3. Shaly Sand Evaluation Using Gamma Ray Spectrometry,
    G. Marett, P. Chevalier, P.Souhuite, J. Suau, SPWLA, 1976.

RECOMMENDED PARAMETERS:
                Range            Default
  GR0        5 to 50        15 API units
  GR100    80 to 150     115 API units
Choose from crossplot or from depth plot.

NON-LINEAR ADJUSTMENT TO CALCULATED SHALE VOLUME
Various studies have shown that the GR, and in some cases the SP, is not a linear prediction of shale volume. Various formulae are used to modify the linearly derived shale volume to obtain a more satisfying answer.

Schlumberger Clavier equation.
         14: IF NONLINSWITCH$ = "CLAVIER"
         15: THEN VSHc = 1.7 - (3.38 - (VSHgr + 0.7) ^ 2) ^ 0.5

Dresser tertiary equation.
       16: IF NONLINSWITCH$ = "TERTIARY"
       17: THEN VSHc = 0.083 * (2 ^ (3.7 * VSHgr) - 1)

Dresser older rock equation.
        18: IF NONLINSWITCH$ = "OLDERROCKS"
        19: THEN VSHc = 0.33 * (2 ^ (2 * VSHgr) - 1)
        19: OTHERWISE Vshc = Vsh

Where:
  VSHgr = shale content from GR or SP (fractional)
  VSHc = shale content corrected for non-linear effects (fractional)

COMMENTS:
Vsh must be within the range of 0.0 to 1.0 before applying these formulae. The Clavier equation is a good compromise between the tertiary and older rock equations. The graph below illustrates these curves.

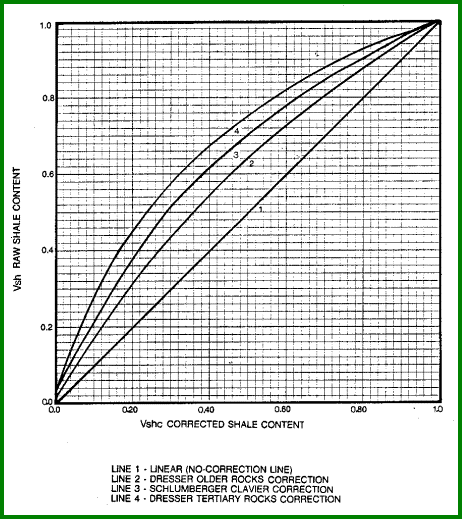
Non-Linear Adjustments to Shale Volume

RECOMMENDED PARAMETERS:
None.

Shale Volume From Spectral Gamma Ray Log - THORIUM
The algebraic formula to solve for shale volume from the gamma ray spectrolog is in the same form as the normal gamma ray.

      20: VSHth = (TH - TH0) / (TH100 - TH0)
        21:  VSHth = Min(1, Max(0, VSHth))

Where:
  TH = gamma ray spectrolog reading in zone of interest, thorium only (ppm)
  TH0 = gamma ray thorium reading in 100% clean zone (ppm)
  TH100 = gamma ray thorium reading in 100% shale (ppm)
  VSHth = shale volume from thorium curve of gamma ray spectrolog (fractional)

COMMENTS:
The gamma ray spectral log thorium curve for shale volume is preferred in dolomites and sandstones which are radioactive due to uranium content, and zones which contain feldspar.

 Shale Volume from Gamma Ray Spectrolog -  Potassium
        22: VSHk = (K - K0) / (K100 - K0)
         23:  VSHk = Min(1, Max(0, VSHk))

Where:
  K = gamma ray spectrolog reading in zone of interest, potassium only (percent)
  K0 = gamma ray potassium reading in 100% clean zone (percent)
  K100 = gamma ray potassium reading in 100% shale (percent)
  VSHk = shale volume from potassium curve of gamma ray spectrolog (fractional)

COMMENTS:
The gamma ray spectrolog potassium curve for shale volume is an alternative method in dolomites and sandstones, which are radioactive due to uranium content. It cannot be used in zones which contain feldspar and its derivatives, such as kaolinite.

Two formulae commonly seen are:

Shale Weight from the Gamma Ray Spectrolog
        24. Wfel = (TH / THCL - K / KCL) / (THFEL / THCL - KFEL / KCL)
         25. Wcl = (TH / THFEL - K / KFEL) / (THCL / THFEL - KCL / KFEL)

Where:
  K = potassium log reading (percent)
  KCL = potassium log reading in 100 % clay (percent)
  KFEL = potassium log reading in 100 % feldspar (percent)
  TH = thorium log reading (ppm)
  THCL = thorium log reading in 100 % clay (ppm)
  THFEL = thorium log reading in 100 % feldspar (ppm)
  Wcl = weight of clay (fractional)
  Wfel = weight of feldspar (fractional)

Volumetric fractions of clay and feldspar can be obtained from the density of each constituent. The method is only practical if the potassium and thorium clay values are represented effectively by the log readings in shale. I have no experience with this method, so I cannot recommend it with confidence,

RECOMMENDED PARAMETERS:
             Range         Default
  TH0       0 to 5          0 ppm 
  TH100   10 to 15      10 ppm
  FEL0      0 to 0.5        0 percent
  FEL100   2.0 to 25      2 percent

NUMERICAL EXAMPLE

1. Vsh from gamma ray log:
    VSHgr = (75 - 45) / (135 - 45) = 0.33

2. Vsh from gamma ray spectrolog thorium curve:
    VSHth = (5 - 0) / (10 - 0) = 0.50

3. Vsh from gamma ray spectrolog potassium curve:
    VSHk = (1.5 - 0) / (3 - 0) = 0.44

4. If hole size was 400 mm at the shale point, and mud weight was 1250 kg/m3, the GR log would read low    and a correction would be needed:
    GR100 = 135 * (1 + 0.000322 * (1250 - 1000))*(1 + 0.0024*(400 - 203)) = 217 API units
    VSHgr = (75 - 45) / (217 - 45) = 0.18

This is approximately one half the value without the hole correction applied.

Assume Vsh = 0.50 (50%) , apply non-linear corrections.

5. Clavier equation:
    VSHc = (1.7 - (3.38 - (0.50 + 0.7) ^ 2) ^ 0.5 = 0.30

6. Tertiary equation:
    VSHc = 0.083 * (2 ^ (3.7 * 0.50) - 1) = 0.15

7. Older rocks equation:
    VSHc = 0.33 * (2 ^ (2 * 0.50) - 1) = 0.33