|
Imaginary numbers are in the form "bi" where "b" is a non-zero, real number and "i" is defined by i˛ = -1, called the "imaginary unit". An Imaginary number bi can be added to a real number a, to form a "complex number" of the form (a + bi), where a and b are called respectively, the "real part" and the "imaginary part" of the complex number. Imaginary numbers can therefore be thought of as complex numbers where the real part is zero. The square of an imaginary number is a negative real number. The complex conjugate of a complex number has the reverse sign of the original imaginary part. The complex conjugate of (a + bi) is (a - bi).
Real and imaginary parts are additive: (a + bi) + (c
+di) = (a + c) + (b + d)i, and are multiplicative:
Division is accomplished by multiplying the
numerator and denominator by the complex conjugate
of the denominator:
Factoring of polynomials is the process of expressing a given polynomial as a product of other polynomials. The example polynomial above can be factored as (x − 1)(x + 3). A quadratic equation is one in which a term is raised to the power of 2 and other terms are raised to a lower power or a are constants: x2 + 2x − 3 =0 is a quadradic equation. A root, or zero, of a polynomial in a single variable is the value that of x that forces the polynomial to produce a result equal to zero. In the example above, x = 1 and x = -3 are roots or zeros of the polynomial x2 + 2x − 3 = (x − 1)(x + 3) = 0. All real polynomials of odd degree have a real number as a root. Many real polynomials of even degree do not have a real root.
A
polynomial of degree n will have n roots. Roots are
not always obvious. The roots of a quadratic
equation are found with: Roots of higher order equations are solved by graphing or iterative "solver" software.
Linear simultaneous equations - see
Cramer's Rule.
A point shows position.
A line is infinite and straight and is a set of continuous points that extend indefinitely in either of its direction. A line segment is part of the straight line between two points. Parallel lines do not cross.
A ray is the part of the line which consists of a given point and the set of all points on one side of that point.
An angle can be defined as two rays or two line segments having a
common end point. The endpoint becomes known as the vertex.
An angle occurs when two rays meet or unite at the same
endpoint. The intersection of two plones is a line.
|
||||||||||||||||||||||||||||||||
|
Table of Common
Angles
|
|||||
|---|---|---|---|---|---|
| Angle | 0 | 30 | 45 | 60 | 90 |
| sin^2(a) | 0/4 | 1/4 | 2/4 | 3/4 | 4/4 |
| cos^2(a) | 4/4 | 3/4 | 2/4 | 1/4 | 0/4 |
| tan^2(a) | 0/4 | 1/3 | 2/2 | 3/1 | 4/0 |
Given
Triangle abc, with angles A,B,C; a is opposite to A, b oppositite B,
c opposite C:
Then: a / sin(A) = b / sin(B) = c / sin(C)
c^2 =
a^2 + b^2 - 2ab cos(C) Law of Sines
b^2 = a^2
+ c^2 - 2ac cos(B)
a^2 = b^2
+ c^2 - 2bc cos(A) Law of Cosines
(a - b)/(a + b) = tan
1/2(A-B) / tan 1/2(A+B) (Law of
Tangents)
 Hyperbolic Definitions
Hyperbolic Definitions
sinh(x) = ( ex - e-x )/2
csch(x) = 1/sinh(x) = 2/( ex - e-x )
cosh(x) = ( e x + e -x )/2
sech(x) = 1/cosh(x) = 2/( ex + e-x )
tanh(x) = sinh(x)/cosh(x) = ( ex - e-x )/( ex
+ e-x )
coth(x) = 1/tanh(x) = ( ex + e-x)/( ex
- e-x )
cosh2(x) - sinh2(x)
= 1
tanh2(x) + sech2(x) = 1
coth2(x) - csch2(x) = 1
 Inverse Hyperbolic Defintions
Inverse Hyperbolic Defintions
arcsinh(z) = ln( z +
![[sqrt] [sqrt]](../All-Images/text119fp/sqrt.gif) (z2
+ 1) )
(z2
+ 1) )
arccosh(z) = ln( z
![[sqrt] [sqrt]](../All-Images/text119fp/sqrt.gif) (z2
- 1) )
(z2
- 1) )
arctanh(z) = 1/2 ln( (1+z)/(1-z) )
arccsch(z) = ln( (1+![[sqrt] [sqrt]](../All-Images/text119fp/sqrt.gif) (1+z2)
)/z )
(1+z2)
)/z )
arcsech(z) = ln( (1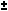
![[sqrt] [sqrt]](../All-Images/text119fp/sqrt.gif) (1-z2)
)/z )
(1-z2)
)/z )
arccoth(z) = 1/2 ln( (z+1)/(z-1) )
 Relations to Trigonometric Functions
Relations to Trigonometric Functions
sinh(z) = -i sin(iz)
csch(z) = i csc(iz)
cosh(z) = cos(iz)
sech(z) = sec(iz)
tanh(z) = -i tan(iz)
coth(z) = i cot(iz)
 Spherical Trigonometry
Spherical Trigonometry
Spherical trigonometry is a
branch of spherical geometry which deals with polygons (especially
triangles) on the sphere and the relationships between the sides and
the angles. This is of great importance for calculations in
astronomy and earth-surface, orbital and space navigation.
On the surface of a sphere, the closest analogue to straight lines are great circles, i.e. circles whose center coincide with the center of the sphere. As with a line segment in a plane, an arc of a great circle (subtending less than 180°) on a sphere is the shortest path lying on the sphere between its two endpoints. An area on the sphere, bounded by arcs of great circles, is called a spherical polygon.
The sides of these polygons are specified not by their lengths, but by the angles at the sphere's center subtended by the endpoints of the sides. Note that this arc angle, measured in radians, when multiplied by the sphere's radius equals the arc length.
 The
sum of the vertex angles of spherical triangles is always larger
than the sum of the angles of plane triangles, which is exactly
180°. The amount E by which the sum of the angles exceeds 180° is
called spherical excess:
The
sum of the vertex angles of spherical triangles is always larger
than the sum of the angles of plane triangles, which is exactly
180°. The amount E by which the sum of the angles exceeds 180° is
called spherical excess:
E = A + B + C - pi
where A, B, and C denote the
angles.
This surplus determines the surface area of any spherical triangle:
A = R2 * E
where R is the radius of the sphere.
 Identities
Identities
Click Here (mathworld.wolfram.com)
Copyright 2023 by Accessible Petrophysics Ltd.
CPH Logo, "CPH", "CPH Gold Member", "CPH Platinum Member", "Crain's Rules", "Meta/Log", "Computer-Ready-Math", "Petro/Fusion Scripts" are Trademarks of the Author



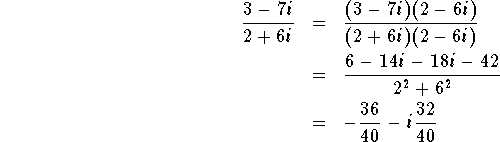
 A polynomial is an expression that is constructed
from one or more variables and constants, using only
the operations of addition, subtraction,
multiplication, and exponentiation. For example, x2 + 2x − 3 is a polynomial in
the single variable x.
A polynomial is an expression that is constructed
from one or more variables and constants, using only
the operations of addition, subtraction,
multiplication, and exponentiation. For example, x2 + 2x − 3 is a polynomial in
the single variable x. Plane
geometry is the study of angles and triangles, perimeter, area and
volume. It differs from algebra in that it develops a logical
structure where mathematical relationships are proved and applied.
Euclid (c. 300 BCE) introduced certain axioms, or postulates,
expressing primary or self-evident properties of points, lines, and
planes. He proceeded to rigorously deduce other properties by
mathematical reasoning. Some of these are listed below.
Plane
geometry is the study of angles and triangles, perimeter, area and
volume. It differs from algebra in that it develops a logical
structure where mathematical relationships are proved and applied.
Euclid (c. 300 BCE) introduced certain axioms, or postulates,
expressing primary or self-evident properties of points, lines, and
planes. He proceeded to rigorously deduce other properties by
mathematical reasoning. Some of these are listed below.
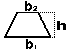
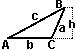
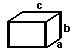
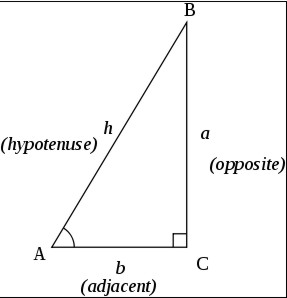 The
trigonometry functions are defined by a right triangle with angle
theta, adjacent side b, oposite side a, and hypotenuse c.
The
trigonometry functions are defined by a right triangle with angle
theta, adjacent side b, oposite side a, and hypotenuse c.