Please be fair to the author. Pay your Shareware fee HERE, and receive the CD-ROM at no extra cost.

	This Page è	Gamma Ray Basics	GR Detectors	Spectral Gamma Ray Logs
	See Also  è	Atomic Physics	Mineral Props	Courses	Site Map

GAMMA RAY BASICS
Gamma ray logs are recorded in virtually every oil and gas well drilled, and on most logs run in mineral exploration prospects. In sedimentary rocks, shales are often more radioactive than reservoir rocks such as sandstone, limestone, and dolomite (although there are exceptions). The shape of the gamma ray log with respect to depth assists in correlating layers from one well to another, and for assessing depositional environment.

Of the 117 elements, 83 have more than one form, or isotope. Isotopes are inherently unstable and, over time, decay to the lower energy, stable form. The half life of an isotope may be millions of years, days, or even milliseconds.

The most common isotopes are the uranium series, the thorium series, and potassium, which has only one unstable isotope. These elements are found in nature, and amongst other things, emit natural gamma rays that can be detected by a logging tool in a borehole.

Each of the above elements naturally emits gamma rays which are distinctive in both number and energy. One gram of potassium 40 emits an average of 3.4 photons per second at a fixed 1.46 MeV energy. But an equal weight of either thorium or uranium produces respectively 12,000 or 26,000 gamma rays per second with a spectrum of energies that average 0.5 MeV.

In the logging industry, gamma ray flux has been recorded in micrograms Radium equivalent per ton (ug Ra equiv / ton) prior to about 1960. After that time, logs were calibrated in API units based on known radiation levels of artificial formations in test pits located in Houston. The usual scale for old style logs was 0 to 10 ug Ra and 0 to 100, 0 to 120, or 0 to 150 API units for newer logs. There is an exact conversion between ug Ra and API units but since the old logging tools were rarely calibrated, this conversion is seldom useful. The pragmatic solution is to multiply ug Ra by 10 to obtain an approximate API units scale.

The counting rate at the detector in a gamma ray logging tool is naturally influenced by the tool itself and the borehole environment. However, the primary response will be related to the number of atoms per unit mass emitting gamma rays.

Therefore, the effective gamma ray response due to potassium 40, for a single compound is:
      1: GRk = 6.02*10^23 * Nk * C / M

WHERE:
  C = 0.000118 (relative abundance of K40 to K39)
  GRk = number of gamma ray emissions
  M = molecular weight of the rock
  Nk = number of potassium atoms per gram

For a mixture:
      2: GRk = Sum (Wi * GRki)

WHERE:
  GRki = gamma ray contribution of ith component
  Wi = weight fraction of the ith component

An empirical relationship between effective potassium content and gamma ray API units is reproduced  below for the standard gamma ray logging conditions of 8" borehole, 10 lb/gal mud and 3 5/8" scintillation NaI detector type tool typical of the 1960 - 1980 era. Newer tools are more sensitive and more linear. This relationship was originally developed by the author while calibrating gamma ray log response to potash ore content of sylvite beds in 1963. For other borehole environments refer to appropriate borehole correction charts.

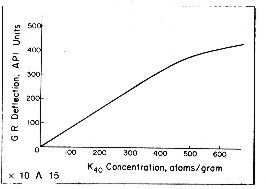Some tools are more linear than this one. The flattening effect at high count rates is due to the dead time of the detector system. Dead time is the time it takes to measure and transmit the recorded pulse to the surface. For other tool types, with different detectors and dead times, the relationship must be found by calibration.

 

GAMMA RAY DETECTORS
Four basic types of gamma ray detectors have been used since the inception of radiation logging. These are ionization chambers, Geiger-Mueller detectors, proportional counters, and scintillation detectors. Although proportional counters are presently used only in neutron logging, the remaining three types have been commonly used to make either gamma ray or neutron measurements.

The first three types operate on the general principle of gas ionization caused by incident gamma rays. Most middle aged and modern tools use scintillation counters composed of sodium iodide (NaI) crystals. These emit a tiny flash of light when struck by a gamma ray. The flash of light is amplified by a photo-multiplier tube, which in turn generates an electrical pulse. Thr pulses are counted by appropriate electronics to provide the gamma ray count rate recorded on the log.

Scintillation detectors are more efficient than gas detectors because they contain a greater mass of radiation sensitive material. Also, their relatively small size enables them to resolve thin beds much more accurately. Scintillation detectors provide adequate resolution in formations as little as three feet thick.

GAMMA RAY SPECTRAL LOG
Pulse size depends on the amount of energy absorbed from the gamma ray. Thus the gamma rays can be sorted by their energy level, leading to the concept of a spectral gamma ray log.

In gamma ray spectral logging, the three main gamma ray contributors, potassium, thorium, and uranium, give gamma rays of different energy levels. By appropriate filtering, the total gamma ray flux can be separated into the three components. This aids petrophysical analysis as thorium is a good shale indicator when uranium masks the total GR response. Thorium-potassium ratio and other combinations of curves can be used for mineral identification and clay typing. Finally, uranium counts can be subtracted from the total counts to give a uranium corrected gamma ray curve that is easier to use and to correlate from well to well.

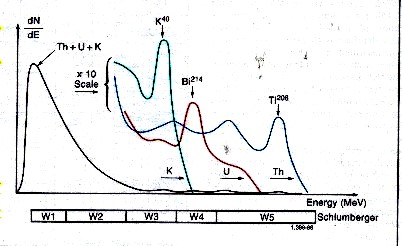
Spectral breakdown of total GR into five energy windows, leading to the segregation
of total counts into three major components - potassium, thorium, and uranium.

Gamma rays emitted by the formation rarely reach the detector directly. Instead, they are scattered and lose energy through three possible interactions with the rocks; the photoelectric effect, Compton scattering, and pair production. Because of these interactions and the response of the sodium iodide scintillation detector, the spectra are degraded to the rather “smeared” spectra shown above.

The high-energy part of the detected spectrum is divided into three energy windows, W1, W2, and W3; each covering a characteristic peak of the three radioactivity series. Knowing the response of the tool and the number of counts in each window, it is possible to determine the amounts of thorium 232, uranium 238, and potassium 40 in the formation. There are relatively few counts in the high-energy range where peak discrimination is best; therefore, measurements are subject to large statistical variations, even at low logging speeds.

By including a contribution from the high-count rate, low-energy part of the spectrum (Windows W4 and W5), these high statistical variations in the high-energy windows can be reduced by a factor of 1.5 to 2. The statistics are further reduced by another factor of 1.5 to 2 by using a filtering technique that compares the counts at a particular depth with the previous values in such a way that spurious changes are eliminated while the effects of formation changes are retained.
 

Copyright © E. R. (Ross) Crain, P.Eng.  email
Read the Fine Print