OHM'S LAW
All resistivity logs obey Ohm's Law (one way or another), as well as the series and parallel circuit concepts defined here.
 

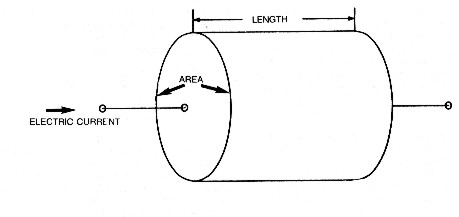
Electrical resistance is the property of a material to resist the passage of electric current through the material. If a voltage, sometimes called a potential or electromotive force, is applied to two sides of a chunk of material, such as wire, a piece of rock, or an electrical appliance, electric current flows through the material. The resistance is defined by Ohm's Law (Georg Ohm, 1827), for direct current (DC) systems, as the ratio of the voltage applied to the current that flows:
    1: R = V / I

Where:
  V = voltage (volts)
  I = current (amperes)
  R = resistance (ohms)

It is interesting to note that the units of measurement for electrical potential, current, and resistance (volt, ampere, ohm respectively) were not established until 1863, some 36 years after Ohm's publication. Prior to this date, and for some time afterward, more than a dozen units of measurement of resistance were in use by the infant science of telegraphy, including such arcane terms as a "German mile", referring to a particular length of a wire of a particular composition and cross-sectional area.

To become consistent with metric units, the actual value of an ohm was varied several times, most recently in 1948 and again in 1972.

Ohm's Law has been extended to alternating current  (AC) systems as:
    2: Z = V / I

Where:
  V = voltage (rms volts or instantaneous volts)
  I = current (rms amperes or instantaneous amperes)
  Z = impedance (ohms)

This looks like Ohm's Law but V and I are vectors represented by complex numbers, so Z is also a complex number. Reactive and capacitive elements in the circuit cause phase shifts between V and I. Z will not be the same as R except in purely resistive circuits.

The term "rms" means "root mean square", a method for averaging the absolute values of instantaneous voltage or current over time to obtain a useful value with a meter. A pure sine wave AC voltage of 10 volts rms will have a peak voltage of +/-14.1 volts.

The current in a DC circuit is dissipated as heat in the resistor, but only the real component of the complex current is dissipated in an AC system. The imaginary component is converted to a magnetic field in the reactive element.

Schlumberger and Lane Wells used DC circuits in their Electrical Logs (actually an alternating DC square wave to prevent polarization of the electrodes). Halliburton and Welex used AC circuits. Given identical electrode arrangements, both would give identical results in an infinite homogenous rock, but thin beds or laminated rocks could provide capacitive effects, detrimental to the AC system.

RESISTIVITY and CONDUCTIVITY
Resistivity is the resistance of a unit volume of a material. In the metric system, the unit of length is the meter, and area is the square meter. Thus, resistivity is measured in units of Ohm - meters squared per meter (Ohm-m2/m), often abbreviated as Ohm-m. Resistivity also equals the ratio of voltage to current, if the length and area are unity. Thus:
    3: RES = V / I * L / A

Where:
  A = area (square meters)
  V = voltage (volts)
  I = current (amperes)
  L = length (meters)
  RES = resistivity (ohm-m)

RES = V / I * L / A

Conductance is the inverse of resistance:
    4: C = 1 / R

Where:
  C = conductance (siemens)
  R = resistance (ohms)

Units of conductance are measured in Siemens, named after an early electrical pioneer. The previous name of the unit of conductance was mho, the reverse spelling of Ohm.

Conductivity is the inverse of resistivity:
    5: COND = 1 / RES

Where:
  COND = conductivity (S/m)
  RES = resistivity (ohm-m)

The units of conductivity are Siemens-meters per square meter, or Siemens/meter (abbreviated S/m). The old name was mho/meter. In well logging, conductivity is usually given in milli-mho/m or milli-Siemens/m (mS/m), where milli stands for 1/1000, so the equation in common use is:.
    6. COND = 1000 / RES

Many people neglect to write or say the "per meter" part of the units when referring to conductivity and the "meter" part of resistivity. Do not confuse resistivity with resistance just because the units have been incorrectly or inadvertently abbreviated. The word "ohm" was often abbreviated with the Greek letter omega (Ω).

Range of resistivity values in the earth

PARALLEL and SERIES CIRCUITS - KIRCHOFF'S LAWS
When combining the effects of two or more resistances or resistivities, one must distinguish between series and parallel circuits, as shown below. The total resistance or resistivity of items connected in series, is the sum of their resistances or resistivities:
    7: RTOTAL = R1 + R2 + ..... + Rn = Sum (Ri)

Series and Parallel resistance

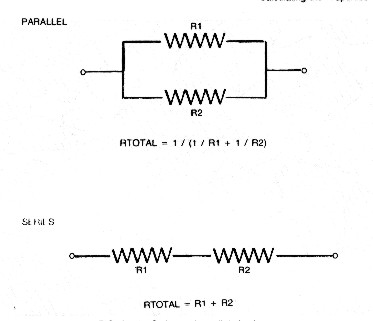
The total resistance of resistances connected in parallel is the inverse of the sum of the inverse of each resistance.
    8: RTOTAL = 1 / (1 / R1 + 1 / R2 + .... + 1 / Rn) = 1 / Sum (1 / Ri)

This is more easily seen as the inverse of the sum of the conductance.
    9: RTOTAL = 1 / (C1 + C2 + .... + Cn) = 1 / Sum (Ci)

These relationships are laws of physics within the pressure and temperature domain of interest to log analysts. Superconductivity does not occur in our realm.

Resistivity is summed in the same manner as resistance - that is, the laws for series and parallel circuits must be obeyed.

Numerical Example
1. Series Circuit:
    R1 = 1 ohm
    R2 = 10 ohm

    RTOTAL = 1 + 10 = 11 ohm
    C = 1/R = 0.9 siemens

    RES1 = 1 ohm-m
    RES2 = 10 ohm-m

    RESTOTAL = 1 + 10 = 11 ohm-m
    COND = 1 / RES = 0.9 siemens/m

2. Parallel Circuit:
    R1 = 1 ohm
    R2 = 10 ohm

    RTOTAL = 1 / (1 / 1 + 1 / 10) = 0.9 ohm
    C = 1 / R = 1.1 siemens

    RES1 = 1 ohm-m
    RES2 = 10 ohm-m

    RESTOTAL = 0.90 ohm-m
    COND = 1.1 siemens/m