|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Please be fair to the author. Pay your Shareware fee HERE, and receive the CD-ROM at no extra cost. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
SONIC VELOCITY -- BASICS
Elasticity is a property of matter, which causes it to resist deformation in volume or shape. Hooke's Law, describing the behavior of elastic materials, states that within elastic limits, the resulting strain is proportional to the applied stress. Stress is the external force (pressure) applied per unit area, and strain is the fractional distortion which results because of the acting force. The modulus of elasticity is the ratio of stress to strain. Three types of deformation can result, depending upon the mode of the acting force. The three elastic moduli are: Young's Modulus, Bulk Modulus, Shear Modulus, Where F/A is the force per unit area and dL/L, dV/V, and tanX are the fractional strains of length, volume, and shape, respectively. Another
important elastic constant, called Poisson's Ratio, is defined
as the ratio of strain in a perpendicular direction to the
strain in the direction of extensional force, Velocity of sound in a material depends on these elastic parameters. Sound can be propagated in rocks with several possible modes. On the surface of the earth, various wave modes are generated by earthquakes and can cause severe damage. In a borehole, a logging instrument emits a sharp sound pulse, which transmits through the rock, again with several modes of transmission. The most useful are the compressional, shear, and Stoneley waves, the first two being transmitted as both body waves inside the rock and surface waves along the wellbore face. The measurements made by a sonic log are recorded in units of travel time, although a velocity scale may be superimposed on some older logs. Geophysicists use velocity values derived from seismic or well log data to assist in their analysis of depth, lithology, porosity, and hydrocarbon indications. Petrophysicists use the inverse of velocity for porosity, lithology, and hydrocarbon analysis.
Velocity is derived from travel time by the equations:
WHERE: The conversion factor of 10^6 accounts for the conventional units of measurement on the sonic log – microseconds per meter (or foot).
The composite compressional
bulk modulus of fluid in the pores (inverse of fluid
compressibility) is:
The pore space bulk
modulus (Kp) is derived from the porosity, fluid, and matrix
rock properties: The
composite rock/fluid compressional bulk modulus is: Compressional and shear
velocity (or travel time) depend on density and on the elastic
properties, so we need a density value that reflects the actual
composition of the rock fluid mixture: Compressional velocity (Vp) and shear
velocity (Vs) are defined as: Although it is not always a precise solution, we often invert equations 5 and 6 to solve for Kb and N from sonic log compressional and shear travel time values. WHERE:
The Biot-Gassmann approach looks deceptively simple. However, the major
drawback to this approach is the difficulty in determining the
bulk moduli, particularly those of the empty rock frame (Kb and
N), which cannot be derived from log data. Murphy (1991)
provided equations for sandstone rocks (PHIe < 0.35) that
predict Kb and N from porosity: These can help overcome the lack of empty rock-frame data. NOTE: Abbreviations used in the literature for elastic constants vary dramatically and no consistent set was found. The abbreviations used in this Handbook reflect those used in recent Schlumberger papers. CAUTION: This book uses the abbreviation "V" for Velocity AS WELL AS for Volume, as in Vsh for volume of shale (not velocity of shale or shear velocity). Likewise the abbreviation K is used for permeability (eg Kmax, Kv, Kh, etc) as well as for compressional bulk modulus. Watch the context! IMPORTANT NOTE: The mechanical properties theory is based on the assumption that rocks behave elastically and are isotropic. Neither of these assumptions is actually true in many situations. Anisotropic behaviour is common and fractured rocks may not behave elastically The nuts and bolts of the above equations shows three
things: It is the last fact that suggests that a log of acoustic velocity or specific acoustic travel time (sometimes called "slowness") might be a reasonable predictor of porosity.
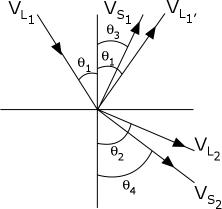
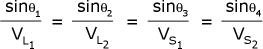
Snell's Law applies to all electromagnetic waves as well as acoustic waves.
The critical angle is the angle of incidence that
creates refraction of sound energy along the interface between two
dissimilar media, for example along the wellbore face (as in well
logging) or along the boundary between two rock layers (as in
seismic refraction surveys). The equation is: Sonic logging tools consist of one or more sources of pulsed sound energy and a number of sound detectors. The sound travels from the source on the logging tool, through the mud in the borehole, to the rock. Here it is refracted at the critical angle, according to Snell’s Law, and travels in the rock parallel to the borehole. The source creates a compressional wave through the mud, a portion of which undergoes mode conversion to create a shear wave as well as the compressional wave in the rock. The shear wave is slower than the compressional, and modern sonic log processing can segregate and record both. Both compressional and shear waves refract back into the borehole, the shear converting to a compressional wave, to be detected by the receivers in the logging tool.
WHERE: Note that V is a Velocity here, while V is used as Volume elsewhere in this Handbook. Example:
WHERE: Cw must usually be found from laboratory measurements. Example: Vwater
= ((144 * 32.17) / (2.0*10^-6 * 78.80 )) ^ 1/2 = 5,450 ft/sec
WHERE: The
transverse (shear) wave velocity is defined by the following two
equations: WHERE: To translate these formulae into metric, convert density into gm/cc, velocity to Km/sec and the various moduli to megabars, and change the constant terms to 1.0. To convert moduli in megabars to psi, multiply by 6.89 * 10^-6. To convert megabars to Kilopascals, multiply by 10^4. Also note that 1 GigaPascal (GPa = 10^10 dynes/cm^2.
WHERE: This is called the Wyllie time average equation and is true for many situations where the components are not very compressible, such as oil, water, sandstone, and shale. It does not work too well with gas under low pressure. This formula is an empirical relationship and is not rigorous, and is therefore, not a law of physics. The
expansion of this formula for log analysis parallels the density
formula:
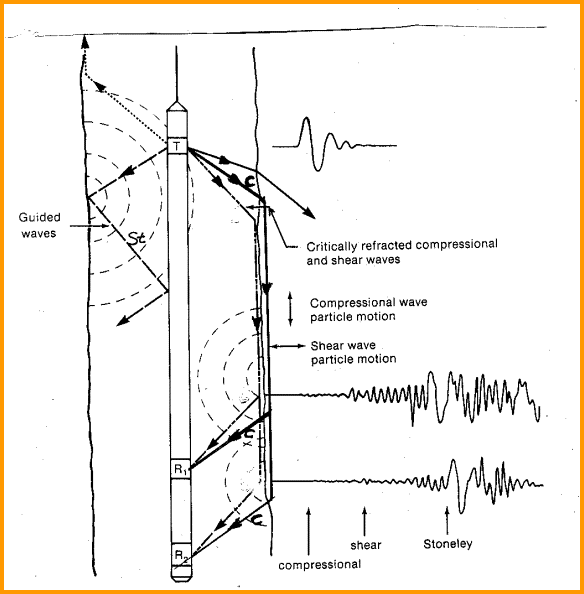
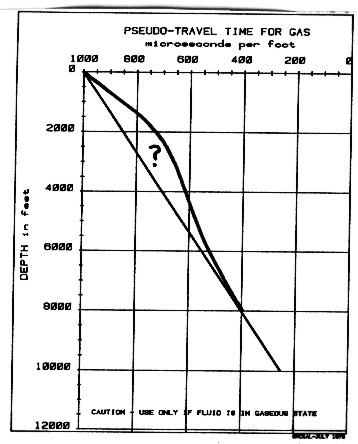
This expansion works well as a predictive tool with oil or water in the porosity, as the travel time of sound in liquids is quite predictable. Equation 21: Vgas = ((Ks * P) ^ 1/2) / DENS, where K is ratio of specific heats and P is pressure, looks like a good solution for finding DTCh for gas zones. However Ks is not usually available and some other solution is often needed. The Biot-Gassmann equations are often preferred, empirical values for DTCh are also used, as in the graph at the right..
What percent change in velocity could be expected if 75% of the pore space were filled with methane gas? 0.
Convert velocity to cm/sec. 1.
Invert the velocity equation and solve for Kc (sometimes referred
to as the space modulus M) for 100% water-bearing condition. 2.
Determine Km from handbook data. For this example, Km was estimated to be 74.5 * 10^10 dynes/cm2 (74.5 GPa) because the rock was a mixture of limestone and dolomite. 3.
Estimate Kb. 4.
Determine fluid properties at reservoir conditions. Water
density = 1.085 gm/cc. Gas-water
combination properties. Kf
from the Wood equation. 5.
Solve Gassmann equation for Kb at Sw = 100%. 6.
Solve this equation for Kc with combination gas/water conditions. 7.
Solve density equation for gas/water combination. 8.
Solve for Vp for Sg = 0.75. Utilizing this methodology and the stated assumptions, there would be an approximate 10% change in velocity (14,000 - 12,500 / 14,000) from a 100% water saturated zone to one that has identical rock properties but 75% gas saturation in the pore space. As a matter of interest, if the rock frame compressibility were assumed to be 5.0 * 10^-7 psi-1, the computed gas/water-bearing velocity would be 13,100 ft/sec. This is only 7% slower than the observed water-bearing velocity and helps demonstrate the sensitivity of the calculation to the assumption of rock frame modulus.
What
percentage change in velocity could be expected if 75% of the
pore space were filled with methane gas (gas gravity 0.8)? Compressibility
values on poorly consolidated formations are difficult to obtain.
It is believed that many operators are attempting to measure and
catalogue such data. However, most of these data are being held
confidential. The velocity change computed with these assumptions is approximately 34%. However, the computed velocity of 5,370 feet per second, or 186 microseconds per foot, compares reasonably well to observed sonic log values in gas zones having rock and reservoir properties similar to the assumptions made in this calculation. As a matter of interest, if the bulk compressibility of the rock frame is assumed to be 3.0 * 10^-5 psi-1, or an increase of nearly an order of magnitude, the computed Gasmann velocity for 75% gas is 5,000 feet per second. This is an additional 4.5% decrease in velocity from the water-bearing case. 3.
Hard Rock Example - Wyllie Solving
the equation: 4.
Soft Rock Example - Wyllie Solving
the equation: Note
that the result depends largely on the choice of gas pseudo-travel
time, and this is subject to some error in judgment. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Copyright ©
E. R. (Ross) Crain, P.Eng.
email |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
WHERE: