Calculating Seismic Wavelets
If a wavelet can be extracted by autocorrelation of a real seismic trace, it should be used to make the synthetic. If this cannot be done, wavelets are generated from equations which describe the frequency content of the wavelet. There are two types - Ricker wavelets are generated directly in the time domain and Klauder wavelets are generated in the frequency domain. Both are called zero phase wavelets and are a minimum delay. That is, the maximum energy is at the beginning of the wavelet. Ricker wavelets are shown below.
 

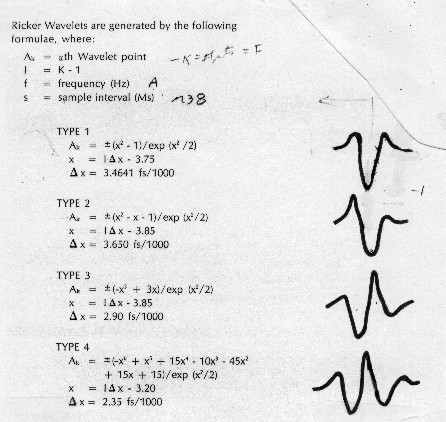
                       Standard computed wavelet shapes                                                                               

There are four different Ricker wavelets, called Ricker Type 1, Type 2, Type 3, and Type 4 respectively. The higher types have more peaks and valleys, representing more "ringing", and are less symmetrical.

Ricker wavelets are used when the synthetic seismogram is to match dynamite or airgun data. They are computed from the following:

Ricker Type 1:
      1: G = 3.4641 * CFREQ / 1000
      2: FOR I = 1 TO WVLTLENGTH / SAMPRATE
      3: X = (I * SAMPRATE - 1) * G - 3.75
      4: Wvlt [I] = (X * X - 1) / EXP (X * X / 2)
      5: NEXT I

Ricker Type 2:
      1: G = 3.65 * CFREQ / 1000
      2: FOR I = 1 TO WVLTLENGTH / SAMPRATE
      3: X = (I * SAMPRATE - 1) * G - 3.85
      4: Wvlt [I] = (X * X - X - 1) / EXP (X * X / 2)
      5: NEXT I

Ricker Type 3:
      1: G = 2.9 * CFREQ / 1000
      2: FOR I = 1 TO WVLTLENGTH / SAMPRATE
      3: X = (I * SAMPRATE - 1) * G - 3.85
      4: Wvlt [I] = (-X^3 + 3 * X) / EXP (X * X / 2)
      5: NEXT I

Ricker Type 4:
      1: G = 2.35 * CFREQ / 1000
      2: FOR I = 1 TO WVLTLENGTH / SAMPRATE
      3: X = (I * SAMPRATE - 1) * G - 3.2
      4: Wvlt [I] = 0.1*(-X^6+X^5+15*X^4-10*X^3-45*X*X+15*X+15)/EXP(X*X/2)
      5: NEXT I

When comparing synthetic seismograms with different wavelets, it is important that each wavelet have the same initial energy. The energy can be found by squaring and summing each of the Wvlt[I] terms. The sum is then compared to a standard energy of 1.0 and a scale factor derived, which is multiplied against each Wvlt[I] term to obtain normalized wavelet values.

The Klauder wavelet is generated in the frequency domain, which gives the amplitude and phase spectra of the wavelet. The autocorrelation of the spectra produces the wavelet shape in the time domain. This wavelet is used when the synthetic is to match Vibroseis data.

Klauder Wavelet:

STEP 1: Generate chirp signal amplitude and phase
      1: CFREQ = 0.5 * (LFREQ + HFREQ)
      2: KLFREQ = (HFREQ - LFREQ) / SWEEPLENGTH
      3: K = SAMPRATE / 1000
      4: FOR I = 1 TO SWEEPLENGTH / K

Calculate phase
      5: I[I] = 2 * PI * (LFREQ * I * K + KLFREQ * I * I * K * K / 2) + INITPHASE

Calculate amplitude
      6: R[I] = 1250 * COS(I[I])

Put phase in all 4 quadrants
      7: I[I] = TAN (I[I])
      8: I[I] = ATN (I[I])
      9: I[I] = I[I] * 180 / PI + 180 * (SIN (I[I]) < 0) + 90
      10: NEXT I

STEP 2: Calculate autocorrelation to get wavelet in time domain. This double nested loop takes the first 100 data points and cross correlates them with the last 100 data points of the sweep. Since the number of data points is small, there is little advantage to using the FFT for the correlation.
      1: I = SWEEPLENGTH / SAMPRATE - 1
      2: K = 1
      3: FOR J = SWEEPLENGTH/SAMPRATE TO SWEEPLENGTH/SAMPRATE - 100 BY -1
      4: Auto[K] = 0
      5: FOR L = 1 TO J
      6: Auto[K] = R[L] * R[I - J + L] + Auto[K]
      7: NEXT L
      8: K = K + 1
      9: NEXT J

To see the wavelet shape, the correlation string is reversed and paired with itself:
      10: FOR I = 1 to 100
      11: Wvlt[I] = Auto[100 - I + 1]
      12: NEXT I
      13: FOR I = 101 TO 199
      14: Wvlt[I] = Auto[I - 99]
      15: NEXT I