|
 Permeability CALCULATIONS
Permeability CALCULATIONS
The sixth step in a log analysis is to estimate
permeability and productivity. These values determine whether a
zone is commercially attractive. There are a number of methods
for calculating matrix permeability.
Although it is not a quantitative measure of
permeability, the separation between the two microlog curves is
an excellent indicator. The log can still be run today as part
of a density log survey.
Log analysis matrix permeability is calibrated to maximum
core permeability (absolute permeability or air
permeability). Allowance must be made to eliminate fractured
samples from the core data set. Permeability to liquids is
lower than absolute permeability. Flow capacity from logs (KH)
can be compared to pressure buildup analysis. Again
fractures will cause a difference.
 Permeability From the Wyllie-Rose Method
Permeability From the Wyllie-Rose Method
The general form of this equation has been used by many authors,
with various correlations between log and core data. Individual
analysts routinely calibrate their core and log data to this
equation.
STEP 1: Calculate permeability
1: PERMw =
CPERM * (PHIe ^ DPERM) / (SWir ^ EPERM)
If we recall that SWir = KBUCKL / PHIe, we see
that this equation is strictly a function of porosity if KBUCKL
is a constant. However, KBUCKL varies with shale volume and
grain size, so Perm will vary also.
he permeability from the Wyllie method (PERMw)
is called the effective permeability, Perm. The result is in
millidarcies. It can be calibrated to air, absolute,
maximum, or Klinkenberg corrected permeability from core
analysis, You should state which type of core analysis you
calibrated to.
 USAGE RULES:
USAGE RULES:
·
Use anytime, usually when no core data is
available.
·
Not reliable in fractures or heterogeneous
reservoirs.
·
Calibrate to core by adjusting CPERM, DPERM, and
EPERM. Sw, PHIe and Vsh should have been accomplished earlier.

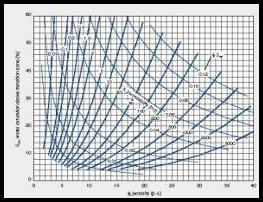 PARAMETERS: PARAMETERS:
RESEARCHER
CPERM
DPERM
EPERM
*
OIL or WATER GAS
Morris-Biggs 65000
6500
6.0
2.0
Timur
6500 650
4.5
2.0
Values of CPERM as low as 10 000 and as high as 1
000 000 have been used in the Morris - Biggs equation. It is
also called the Tixier equation.
 Permeability From Porosity
Permeability From Porosity
Permeability is often a semi-logarithmic function
of porosity, unfortunately with a fairly large deviation. Core
data is usually plotted to determine the equation of the best
fit line: it can be calibrated to air, absolute, maximum, or
Klinkenberg corrected permeability from core analysis,
STEP 1: Calculate permeability
1: PERMp = 10 ^
(HPERM * PHIe + JPERM)
The permeability from the Porosity method (PERMp)
is called the effective permeability, Perm. The result is in
millidarcies.
 USAGE RULES:
USAGE RULES:
·
Use anytime that parameters can be calibrated to
core, especially in low porosity.
·
Not reliable in fractures or heterogeneous
reservoirs.
·
A best fit line of the logarithm of core
permeability vs. core porosity is often used to obtain this
relationship for a particular zone.
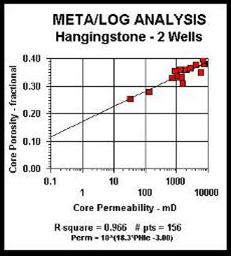  PARAMETERS:
PARAMETERS:
Sandstones
Carbonates
JPERM HPERM
Very
fine grain
Chalky
3.00
16
Fine
grain
Cryptocrystalline-
2.50
18
Medium
grain
Intercrystalline
2.20
20
Coarse
grain
Sucrosic-
2.00
22
Conglomerate
Fine vuggy
1.80
24
Unconsolidated
Coarse vuggy
1.50
26
Fractured
Fractured
1.00
30
The medium grain parameters approximate the
Wyllie - Rose equation. These parameters should be calibrated to
core data whenever possible.
 Permeability From the Coates Method
Permeability From the Coates Method
This is a simplification of an earlier method
proposed by Dumanoir and Coates. It is more optimistic than
other methods in low porosity.
1: PERMc = 5000
* (PHIe ^ 4) * ((PHIt PHIe * SWir) / (PHIe * SWir)) ^ 2
OR in clean zones:
2: PERMc = 5000
* (PHIe ^ 4) * ((1 - SWir) / SWir) ^ 2
Heslop (pere et fils) fitted core data in very
young sediments in two wells and obtained parameters for an
equation similar to the Coates equation (caution: there was no
low or high porosity data in the calibration data set):
3: PERMh = 100
000 * (PHIe ^ 3.9) * (1 - SWir) ^ 3.9
It is clear that the constant and exponents are mutable and
should be calibrated with core data. Equation 3 has the
advantage that low porosity cannot have high permeability,
whereas the other equations that rely on SWir can generate high
perms in low porosity when SWir is extremely low. The
disadvantage is that SWir is needed from capillary pressure
studies, along with the permeability for the same core samples,
in order to calibrate the equation.
The permeability from the Coates method (PERMc)
is called the effective permeability, Perm. The result is in
millidarcies.
 USAGE RULES:
USAGE RULES:
 ·
Use anytime. Porosity method may be better if
core data is available.
·
Use anytime. Porosity method may be better if
core data is available.
·
Not reliable in fractured or heterogeneous
reservoirs.
·
Parameters need to be calibrated to core data for
most zones.
 Fracture Permeability
Fracture Permeability
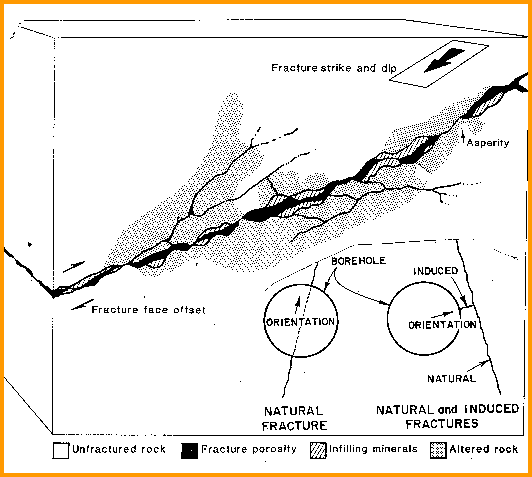 There
are a few published methods for calculating fracture
permeability from conventional open hole logs or from some
arbitrary estimate of fracture porosity. The only correct
approach is to use formation micro-scanner fracture aperture and
frequency data: There
are a few published methods for calculating fracture
permeability from conventional open hole logs or from some
arbitrary estimate of fracture porosity. The only correct
approach is to use formation micro-scanner fracture aperture and
frequency data:
1: Kfrac = 833 *
10^11 * PHIfrac^3 / (Df^2 * KF1^2)
2: Kfrac = 833 *
10^5 * PHIfrac * Wf^2
3: Kfrac = 833 *
10^2 * Wf^3 * Df * KF1
Where: KF1 = number
of main fracture directions
= 1 for sub-horizontal or sub-vertical
= 2 for orthogonal sub-vertical
= 3 for chaotic or brecciated
PHIfrac = fracture porosity (fractional)
Df = fracture frequency (fractures per meter)
Wf = fracture aperture (millimeters)
Kfrac = fracture permeability (md)
Kfrac can be many thousands of millidarcies.
Equations 1, 2, 3 give identical results.
|

