|
 QUANTITATIVE ANALYSIS BASICS
QUANTITATIVE ANALYSIS BASICS
Quantitative
petrophysical analysis is a matter of data reduction and summary,
using the basic laws of mathematics, physics, and chemistry,
coupled with a fair amount of common sense and experience.
Analysis and interpretation should not be confused or construed
to be one and the same. Some people use the words log evaluation
to mean either or both analysis and interpretation. We prefer
to think that analysis and evaluation mean data reduction and
that interpretation involves trying to understand these results
in light of the assumptions made, and other known facts not used
in the analysis.
 With
the advent of modern, inexpensive, multi-function, programmable
calculators, pocket computers, and desktop micro-computers, chartbook
methods are quickly disappearing. Charts are occasionally
referred to when working in complex lithology, where the pattern
or position of points on the chart or graph may be helpful. Even this can be quantified
by appropriate equations. With
the advent of modern, inexpensive, multi-function, programmable
calculators, pocket computers, and desktop micro-computers, chartbook
methods are quickly disappearing. Charts are occasionally
referred to when working in complex lithology, where the pattern
or position of points on the chart or graph may be helpful. Even this can be quantified
by appropriate equations.
Algebra
from various Chapters can be merged together and coded in calculator
or computer language to give customized programs for the individual
user. Once recorded and documented, they can be carried on the
job as readily as a chartbook, and they are much more convenient
and powerful. Most chartbooks do not handle shale corrections,
so they are now inappropriate for very many oil and gas
reservoirs.
INTEGRATED
PETROPHYSICS
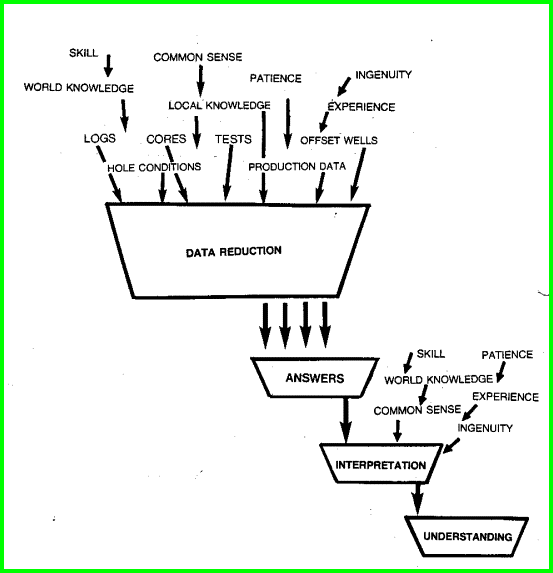
The Data Reduction / Analysis / Interpretation / Understanding Model
for Integrated Petrophysics
For
fast, practical analysis, preprogrammed methods for the calculator
or computer are essential. Spreadsheet software , commercial
petrophysical packages, and in-house software has replaced the
chartbook. Unfortunately, many of these systems are delivered
pretty "naked"; you will probably have to code numerous
equations into the package yourself.
These are provided in later sections
of this Handbook and are "computer-ready". They do not need to
be derived, translated, or heavily modified to be used in virtually all computers with Basic,
Fortran, or similar computer languages or interpreters. This may
have made the equations a little harder to read, but easier to
use.
Not
all methods outlined in this handbook, or elsewhere, apply in
every instance. Nor is there time or data available to try every
method on a particular zone. How to select a reasonable method
is described in appropriate sections of each Chapter.
Most
user defined equation interpreters require that you distinguish
between a log curve and a parameter - read your software
documentation manual to see how this is done and adapt the
algorithms in this Handbook appropriately.
 THE MATH HIERARCHY
THE MATH HIERARCHY
Calculations are performed in a specific order by all
mathematicians and all computers. Analysts using hand calculators or
pencil and paper are obligated to use the same system or will get
erroneous results. The order of the operations is called the
mathematical hierarchy, and is defined as follows:
Highest Priorty
( ) brackets
^, exp
*, /, mod
+, -
= , >, <, < =, > =, #
not
and
or, xor
min, max, sum, avg, log, ln
Lowest
Priority
Operations at the highest priority are performed
first, followed by the next lowest, and so on. If more than one type
of operation is shown at one priority level, they are evaluated from
left to right as found in the equation. The object of the hierarchy
is to reduce the number of brackets needed to indicate the order of
calculation.
EXAMPLES:
A = B + C * D means multiply C by D then add to B
A = B * C ^ D means take C to the power D then multiply by B
A = (B + C) ^ 2 * D means add B and C, square it, then multiply by
D
A = log ((B + C) ^ 2 * D) means add B and C, square it, then
multiply by D, then take the logarithm
A = max (X, Y, B + C - 2 * D) means multiply 2 times D, add B and
C, subtract the product of
2 * D from
the sum of B + C, then decide if this result or X or Y is the
largest value.
NOTE that spaces are not allowed in real computer math - they are
usd here and elsewhere in this Handbook to make the equations easier
to read.
 PETROPHYSICAL ALGORITHMS
PETROPHYSICAL ALGORITHMS
An algorithm is a set of mathematical operations impressed upon
the log data, assumed parameters, and possibly on the results
of previously applied algorithms, which produces one or more easily
defined numerical results. A series of algorithms make up a routine,
and a series of routines make up a computation. Algorithms presented
here are self contained units and do not rely too heavily on previous
algorithms, so some internal duplication exists, especially in
the area of units conversions.
The
layout of all algorithms in this book has been specially designed
to allow a text editor or language interpreter program to convert
the information into a working program. This has been achieved
by using a very brief pseudo-programming language with few keywords,
and yet it retains many components of the English language to
increase readability.
 LAYOUT
OF ALGORITHMS IN THIS BOOK
LAYOUT
OF ALGORITHMS IN THIS BOOK |
| |
1.
Chapter sub-heading - (subject name) |
| |
2.
Introductory text for this subject. |
| |
3.
Algorithm name and abbreviation. |
| |
4.
Mathematical formula, using consistent curve and interpretation
parameter names, preceded by an algorithm line number. |
| |
5.
Dictionary of curve and parameter names, and units of
measure. |
| |
6.
Trailing comments, including recommended usage, and
warnings. |
| |
7.
Recommended values for parameters. |
| |
8.
Numerical example of the algorithm. |
| |
9.
Comments may also be interspersed between each line
of the mathematics, and may act as sub-titles for each
equation. |
| |
|
|
More
than one algorithm may appear under a single Chapter subheading.
Conversely some Chapter subheadings may contain no algorithm.
The
algorithms are written in a pseudo computer language using structural
programming style. The key words are:
IF
AND IF
OR IF
THEN
OTHERWISE (ELSE is used in many computers)
AND
FOR ...TO ...ENDLOOP
Each
keyword follows the algorithm line number, and only one keyword
can be on a line. For example:
1: IF X > Y
2: THEN Z = 36
A
more complicated IF statement might use several lines:
1: IF X > Y
2: AND IF Z > 36
3: OR IF SWITCH$ = "ON"
4: THEN W = 14
5: AND Q = 8
6: OTHERWISE W = 15
7: AND Q = 9
Using
this style eliminates the need for the END IF statement and allows
one to read the program in English without difficulty. It also
lends itself to automatic translation into Excel, Basic or Fortran by
a simple interpreter program or the Find/Replace function of a
word processor. Some language interpreters will insist that the
complete IF..THEN..ELSE be on one program line. Some care is required
to keep the AND and OR statements sorted out when you convert
this pseudo-code. Some languages will insist on different punctuation
or parentheses to compile correctly. Read your language manuals
carefully to determine what you need to do to translate the algorithms.
An
example will illustrate this point more clearly:
 Sample Algorithm Sample Algorithm
|
This
is line one of the sample algorithm.
1: CSZ = RHT + 2.06 * (BITZ - 1)
A line of math may require more than one line of text,
such as this example.
2: CSZ = RHT[] + 2.06 * (BITZ - 1) * (1 - (999 + METR))
/ (1 + 3.28 * (IF KILL$ = "NO"))
The end of an algorithm is signaled by the data dictionary.
Where:
BITZ = bit size (mm or inches)
CSZ = casing zugle (mm or inches)
RHT = relative hot tub temperature (deg C or deg F)
X = intermediate variable
Y = intermediate variable
etc.
 COMMENTS:
COMMENTS:
This example illustrates most of the features of the
pseudo-computer language used in this book. A number,
followed by a colon, cannot be used within the comments
interspersed within the algorithm math section, but
can occur anywhere else in the overall algorithm description.
Note
that log curves are vectors (a mathematical term for
a string of numbers) and parameters (constants for
a zone) are single-valued. Take care to translate
log curves in the pseudo-code appropriately into your
chosen computer language.
 USAGE RULES
USAGE RULES
Use in preference to XXX method when data is
available.
 RECOMMENDED
VALUES FOR PARAMETERS:
RECOMMENDED
VALUES FOR PARAMETERS:
A = 0.62 M = N = 1.78
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
Given BITZ = 205
METR = 1
etc.
|
|
|

