QUANTITATIVE ANALYSIS BASICS
Quantitative petrophysical analysis is a matter of data reduction and summary, using the basic laws of mathematics, physics, and chemistry, coupled with a fair amount of common sense and experience. Analysis and interpretation should not be confused or construed to be one and the same. Some people use the words log evaluation to mean either or both analysis and interpretation. We prefer to think that analysis and evaluation mean data reduction and that interpretation involves trying to understand these results in light of the assumptions made, and other known facts not used in the analysis.

With the advent of modern, inexpensive, multi-function, programmable calculators, pocket computers, and desktop micro-computers, chartbook methods are quickly disappearing. Charts are occasionally referred to when working in complex lithology, where the pattern or position of points on the chart or graph may be helpful. Even this can be quantified by appropriate equations.

Algebra from various Chapters can be merged together and coded in calculator or computer language to give customized programs for the individual user. Once recorded and documented, they can be carried on the job as readily as a chartbook, and they are much more convenient and powerful. Most chartbooks do not handle shale corrections, so they are now inappropriate for very many oil and gas reservoirs.

INTEGRATED PETROPHYSICS

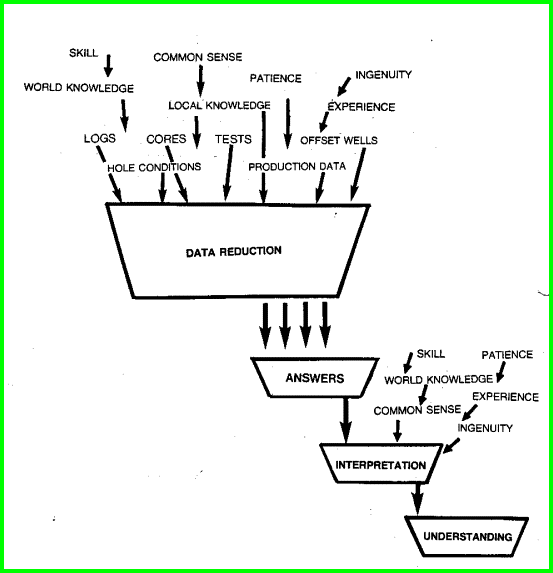
                                                                The Data Reduction / Analysis / Interpretation / Understanding Model for Integrated Petrophysics

For fast, practical analysis, preprogrammed methods for the calculator or computer are essential. Spreadsheet software , commercial petrophysical packages, and in-house software has replaced the chartbook. Unfortunately, many of these systems are delivered pretty "naked"; you will probably have to code numerous equations into the package yourself.

These are provided in later sections of this Handbook and are "computer-ready". They do not need to be derived, translated, or heavily modified to be used in virtually all computers with Basic, Fortran, or similar computer languages or interpreters. This may have made the equations a little harder to read, but easier to use.

Not all methods outlined in this handbook, or elsewhere, apply in every instance. Nor is there time or data available to try every method on a particular zone. How to select a reasonable method is described in appropriate sections of each Chapter.

Most user defined equation interpreters require that you distinguish between a log curve and a parameter - read your software documentation manual to see how this is done and adapt the algorithms in this Handbook appropriately.

THE MATH HIERARCHY
Calculations are performed in a specific order by all mathematicians and all computers. Analysts using hand calculators or pencil and paper are obligated to use the same system or will get erroneous results. The order of the operations is called the mathematical hierarchy, and is defined as follows:

Operations at the highest priority are performed first, followed by the next lowest, and so on. If more than one type of operation is shown at one priority level, they are evaluated from left to right as found in the equation. The object of the hierarchy is to reduce the number of brackets needed to indicate the order of calculation.

EXAMPLES:

 A = B + C * D means multiply C by D then add to B
 A = B * C ^ D means take C to the power D then multiply by B
 A = (B + C) ^ 2 * D means add B and C, square it, then multiply by D
 A = log ((B + C) ^ 2 * D) means add B and C, square it, then multiply by D, then take the logarithm
 A = max (X, Y, B + C - 2 * D) means multiply 2 times D, add B and C, subtract the product of
            2 * D from the sum of B + C,  then decide if this result or X or Y is the largest value.

NOTE that spaces are not allowed in real computer math - they are usd here and elsewhere in this Handbook to make the equations easier to read.

 

 
PETROPHYSICAL ALGORITHMS
An algorithm is a set of mathematical operations impressed upon the log data, assumed parameters, and possibly on the results of previously applied algorithms, which produces one or more easily defined numerical results. A series of algorithms make up a routine, and a series of routines make up a computation. Algorithms presented here are self contained units and do not rely too heavily on previous algorithms, so some internal duplication exists, especially in the area of units conversions.

The layout of all algorithms in this book has been specially designed to allow a text editor or language interpreter program to convert the information into a working program. This has been achieved by using a very brief pseudo-programming language with few keywords, and yet it retains many components of the English language to increase readability.

LAYOUT OF ALGORITHMS IN THIS BOOK   1. Chapter sub-heading - (subject name)   2. Introductory text for this subject.   3. Algorithm name and abbreviation.   4. Mathematical formula, using consistent curve and interpretation parameter names, preceded by an algorithm line number.   5. Dictionary of curve and parameter names, and units of measure.   6. Trailing comments, including recommended usage, and warnings.   7. Recommended values for parameters.   8. Numerical example of the algorithm.   9. Comments may also be interspersed between each line of the mathematics, and may act as sub-titles for each equation.

More than one algorithm may appear under a single Chapter subheading. Conversely some Chapter subheadings may contain no algorithm.

The algorithms are written in a pseudo computer language using structural programming style. The key words are:

    IF
    AND IF
    OR IF
    THEN
    OTHERWISE (ELSE is used in many computers)
    AND
    FOR ...TO ...ENDLOOP

Each keyword follows the algorithm line number, and only one keyword can be on a line. For example:
      1: IF X > Y
      2: THEN Z = 36

A more complicated IF statement might use several lines:
      1: IF X > Y
      2: AND IF Z > 36
      3: OR IF SWITCH$ = "ON"
      4: THEN W = 14
      5: AND Q = 8
      6: OTHERWISE W = 15
      7: AND Q = 9

Using this style eliminates the need for the END IF statement and allows one to read the program in English without difficulty. It also lends itself to automatic translation into Excel, Basic or Fortran by a simple interpreter program or the Find/Replace function of a word processor. Some language interpreters will insist that the complete IF..THEN..ELSE be on one program line. Some care is required to keep the AND and OR statements sorted out when you convert this pseudo-code. Some languages will insist on different punctuation or parentheses to compile correctly. Read your language manuals carefully to determine what you need to do to translate the algorithms.

An example will illustrate this point more clearly: