|
 Water Saturation From The Porosity Water Saturation Product
Water Saturation From The Porosity Water Saturation Product
A handy rule of thumb can be used to estimate water saturation
in many zones. The rule is based on the observation that the product
of porosity and water saturation is constant for a particular
rock type, which is confirmed by core analysis studies. We therefore
do not require knowledge of water resistivity, which is one of
the most difficult interpretation parameters to find.
The concept was originally developed by R. S. Buckles,
published as "Correlating and Averaging (ornate Water
Saturation Data", presented at the 16th Annual Technical
Meeting, P&NG Division, CIMM, Calgary, May, 1965.
The
technique is often called the "Buckles' Number" method, where
Buckles' Number is the product of porosity and irreducible
water saturation. In his original paper,
Buckles proposed that SW = Constant / Porosity. In this Handbook, we
have named the constant KBUCKL and extended the model to shaly sands
by adding a (1 - Vsh) term. In shaly sands the KBUCKL is held
constant at the value for a relatively clean sand and the shale term
effectively varies KBUCKL in proportion to the shaliness.
From
capillary pressure data:
1: KBUCKL = AVG (PHIcore * SWmin)
OR from log analysis data:
2: KBUCKL = AVG (PHIe * SWa)
Averages should be taken over intervals with constant rock type
(pore geometry / grain size and sorting). In the log analysis cae,
some assurance that SWa = SWir is required (eg. clean oil or gas
production with little water).
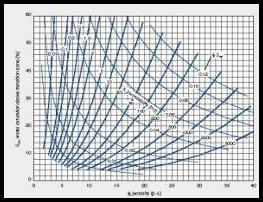
Constant KBUCKL
lines form hyperbolic lines on a porosity vs irreducible
water
saturation crossplot. Permeability usually varies with both PHIe and SWir, shown by diagonal lines on this plot.
Where:
KBUCKL = Buckles' Number (unitless)
SWmin = minimum water saturation on a core plug with porosity PHIcore
(fractional)
SWa = Archie water saturation in a relatively clean zone with porosity
PHIe (fractional)
For
equation 2 to give reasonable results, the zone must be known or
presumed to produce hydrocarbons with little or no water cut on
initial completion. KBUCKL will vary with changes in grain size,
sorting, and overall pore geometry, so a particular value is often
associated with a particular rock type.
A
table of porosity - water saturation products (KBUCKL values) is
listed below in the Recommended Parameters section. Your
own data should be added to the table shown later on this page. Such data can be found
in technical publications and trade journals, from good log analyses
where RW is known, as well as from special core studies (capillary
pressure curves).
Buckles' Number, porosity, irreducible water saturation, and
permeability are intimately linked by the texture and pore geometry
of the rocks, as shown in the crossplot given above.
The
relationship to use to calculate water saturation is:
3: IF PHIe <= 0.0
4: OR IF Vsh >= 0.9
5: OR IF FLUID$ = “WET”
6: THEN SWp = 1.0
7: OTHERWISE SWp = KBUCKL / PHIe / (1 - Vsh)
In all cases:
8: SWir = MIN (1, SWa, SWp)
Where:
PHIe = effective porosity (fractional)
KBUCKL = porosity saturation product (fractional)
SWa = actual water saturation from Archie-type log analysis (fractional)
SWp = water saturation from porosity saturation product (fractional)
Vsh = shale volume (fractional)
 COMMENTS:
COMMENTS:
Use this method when RW is unknown and zone is KNOWN to be hydrocarbon
bearing.
Do
not use in water zones.
The
product of porosity and water saturation, PHI * SW, in many rocks
is a constant, and the product is called Buckles' Number,
after the man who first described this factor.
KBUCKL
is found in a clean hydrocarbon bearing zone with a known RW and
is used in other zones of similar rock types where RW is unknown.
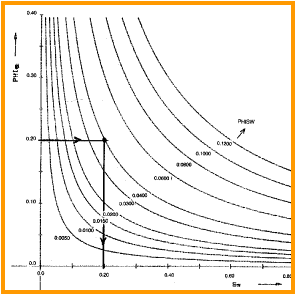 It
can also be found by plotting core porosity vs wetting phase saturation
at an arbitrary capillary pressure from special core analysis
data. It
can also be found by plotting core porosity vs wetting phase saturation
at an arbitrary capillary pressure from special core analysis
data.
If
regression is used to determine SW from PHI, the relationship
is usually hyperbolic (KBUCKL = constant) or a skewed hyperbola
(KBUCKL varies with porosity).
The
shale term has been added by the author to raise KBUCKL and SWp,
automatically for the finer grained nature of shaly sands.
Water saturation from porosity-saturation
product (Buckles
Method) 
Hydrocarbon zones with water saturation (SWa)
above irreducible saturation (SWir) will produce some water
along with hydrocarbons. This can occur in transition zones
between the oil and water leg, or after water influx into a
reservoir due to production of oil or gas.
 PARAMETERS:
PARAMETERS:
Sandstones Carbonates KBUCKL
Very
fine grain Chalky 0.120
Fine
grain Cryptocrystalline 0.060
Medium
grain Intercrystalline 0.040
Coarse
grain Sucrosic 0.020
Conglomerate Fine vuggy 0.010
Unconsolidated Coarse vuggy 0.005
Fractured Fractured
0.001
Gas Shale
0.009 - 0.025
Use these
parameters only if no other source exists.
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
1. For example, if a deep vuggy carbonate has a porosity of 0.10
(10%) and a PHIxSW product of 0.005, then:
SWp = 0.005 / 0.10 = 0.05 (5%)
2.
Assume sands as follows:
| |
Sand
A |
Sand
B |
Sand
C |
Sand
D |
| PHIxSW |
0.04 |
0.06 |
0.06 |
0.08 |
| PHIe |
0.36 |
0.23 |
0.30 |
0.08 |
| SWp |
0.11 |
0.26 |
0.20 |
1.00 |
|

