PYRITE CORRECTIONS
Pyrite is a conductive metallic mineral that may occur in many different sedimentary rocks. It can reduce measured resistivity, thus increasing apparent water saturation. The conductive metallic current path is in parallel with the ionic water conductive path. As a result, a correction to the measured resistivity can be made by solving the parallel resistivity circuit.

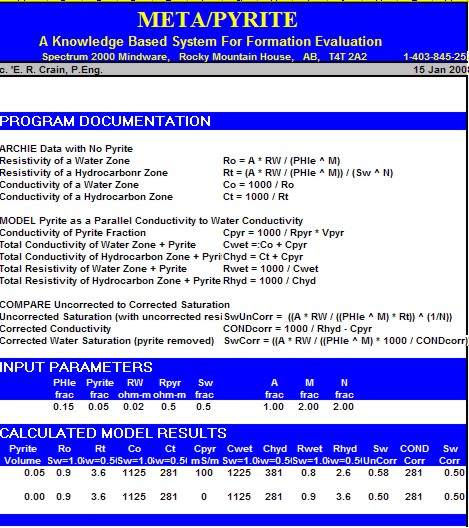
Although the math is simple, the parameters needed are not well known. The two critical elements are the volume of pyrite and the effective resistivity of pyrite. Pyrite volume can be found from a two or three mineral model, calibrated by thin section point counts or X-ray diffraction data.

The resistivity of pyrite varies with the frequency of the logging tool measurement system. Laterologs measure resistivity at less than 100 Hz, induction logs at 20 KHz, and LWD tools at 2 MHz. Higher frequency tools record lower resistivity than low frequency tools for the same concentration of pyrite. The variation in resistivity is caused by the fact that pyrite is a semiconductor, not a metallic conductor. It is nature's original transistor, and formed the main sensing component in early radios.

Typical resistivity of pyrite is in the range of 0.1 to 1.0 ohm-m; 0.5 ohm-m seems to work reasonably well. The effect of pyrite is most noticeable when RW is moderately high and less noticeable when RW is very low.

The math is easiest when conductivity is used instead of resistivity:
     1: CONDpyr = 1000 / RESpyr    
     2: CONDcorr = 1000 / RESD - CONDpyr * Vpyr
     3: RESDcorr = 1000 / CONDcorr

The corrected resistivity can be plotted versus depth, along  with the original log. Corrected water saturation will always be lower or equal to the original Sw. If CONDcorr goes negative, lower Vpyr or raise RESpyr
 

Modeling the Effect of Pyrite
It is often instructive to model the effects of pyrite to see what happens to the resistivity and  water saturation. The method below is aided by a spreadsheet, shown later on this ppage.

Step 1: Model resistivity of water and hydrocarbon zones with no pyrite, using PHIe  from log analysis of the recorded log data, with Sw from capillary pressure or common sense:
     1: Ro = A * RW / (PHIe ^ M)
     2: Rt = (A * RW / (PHIe ^ M)) / (Sw ^ N)

Step 2: Convert these to conductivity
     3: Co = 1000 / Ro
     4: Ct = 1000 / Rt

Step 3: Model conductivity of pyrite and solve for resistivity of water+pyrite and hydrocarbon+pyrite, using parallel circuit theory:
     5: Cpyr = 1000 / Rpyr * Vpyr
     6: Cwet = Co + Cpyr
     7: Chyd = Ct + Cpyr

Step 4: Convert conductivity to resistivity:
     8: Rwet = 1000/ Cwet
     9: Rhyd = 1000 / Chyd
Compare these resistivities to the original Ro and Rt to see the effect of pyrite.

Step 5: To correct an existing log analysis, calculate uncorrected and corrected water saturation:
     10: SwUnCorr = ((A * RW / ((PHIe ^ M) * RESD)) ^ (1/N))
     11: Cpyr = 1000 / Rpyr * Vpyr
     12: CONDcorr = 1000 / RESD - Cpyr
     13: SwCorr = ((A * RW / ((PHIe ^ M) * 1000 / CONDcorr)) ^ (1/N))
Compare SwUnCorr and SwCorr to see the effect of pyrite.

COMMENTS:
The corrected resistivity can be plotted versus depth, along  with the original log.
Corrected water saturation will always be lower or equal to the original Sw.
If CONDcorr goes negative, lower Vpyr or raise Rpyr

RECOMMENDED PARAMETERS:
    Rpyr is in the range 0.1 to 1.0 ohm-m, default 0.5.
    Vpyr is usually in the range 0.00 to 0.08, default 0.03

META/LOG "PYR" SPREADSHEET -- Modeling Pyrite Effect on Resistivity Logs
This spreadsheet models the effects of pyrite on resistivity and saturation values. The model can be used to assess the effect of varying pyrite quantity, pyrite resistivity, water resistivity, and porosity.

Download this spreadsheet:
SPR-09 META/LOG PYRITE CORRECTION CALCULATOR
  Calculate effect of pyrite on resistivity logs.
 

Sample of "META/PYR" Spreadsheet used for modeling the effect of pyrite on resistivity.
 

Resistivity -  Saturation in Laminated Reservoirs
The analysis models for laminated shaly sands are quite varied and none are perfect solutions. This topic is covered more fully elsewhere in this Handbook  The problem lies in how logs average laminations that are thinner than the tool resolution. Most logs average the data in a linear fashion, but resistivity must be averaged as conductivity and then converted back to resistivity. This is the situation with most so-called “low-resistivity” pay zones around the world.

The problem exists in laminated shaly sands and in clean sands or carbonates where porosity is laminated. The shale laminations or the low porosity laminations (with high water saturation) have considerably higher conductivity than the cleaner, higher porosity laminations. The net result is a low resistivity reservoir. The chance of by-passing such zones is quite high.

To illustrate, assume a laminated sequence with shale laminations equal in thickness to the sand laminations. This gives a shale volume (Vsh) averaged over the interval of 50%. Assume the porosity and resistivity values are as shown below:

The resistivity in this gas zone is only 8 ohm-m. It surprises many people that the average of 4 and 200 is only 8! The contrast with the water zone is low, so many laminated zones are bypassed as not being worthy of completion.

In the early days of log analysis, this phenomenon was attributed to many different, almost mystical, reasons because the parallel nature of the conductive paths was not understood by many analysts.

Low resistivity gas pay

In the example above, density neutron crossover shows gas pay in zones with horizontal resistivity of less than 3.0 ohm-m. This crossover is not caused by bad hole conditions or inappropriate density neutron porosity scales. The vertical resistivity shows the effect of the gas, while the horizontal resistivity is dominated by the conductive shale laminations.

While gas zones stand out because of gas effect on the density neutron, oil zones will not be so obvious. Pay attention to sample descriptions, oil shows in core or on the mud pit, and the mud log, especially the higher C4+ curves.

META/LOG "LAM" SPREADSHEET -- Modeling Effects of Laminations
This spreadsheet models the effects of thin laminations of shale in sandstone or thin layers of varying porosity..

Download this spreadsheet:
SPR-16 META/LOG LAMINATED SAND CALCULATOR
 Model laminated shaly sands and laminated porosity.

 

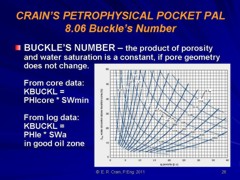
Water saturation cannot be calculated in the usual way in laminated shaly sands. Sometimes porosity cannot be determined explicitly either.

Formation microscanner and acoustic televiewer logs help to obtain a good sand count. Sand porosity is often determined from core analysis and water saturation calculated from the Buckle's method.

Water Saturation in Fractured Rocks
Water saturation in fractured reservoirs is a complex issue and has a huge literature. Fractured reservoirs in general are covered elsewhere in this Handbook, where the dual porosity model for fractured reservoirs is covered. This includes a water saturation method that is widely used.

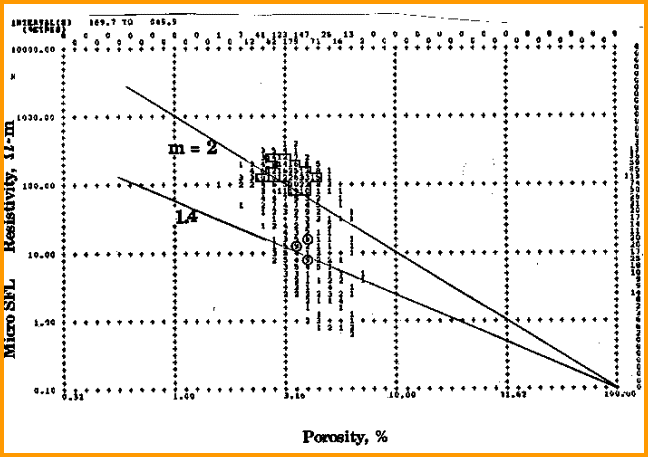
The major complication is that a large fracture will be deeply invaded by mud filtrate and will be full of water at logging time, yet be full of oil or gas at static or producing conditions. The host rock will not invade as deeply so the saturation distribution while logging is not as neat or as predictable as in un-fractured rocks.

In many situations, a simple approach using the Archie water saturation equation with a low value for M is satisfactory. Use the Pickett plot to determine M from a shallow resistivity log. Careful zonation may be required to isolate heavily fractured from less fractured intervals. If M seems to be too high, then the shallow resistivity is seeing residual hydrocarbons.

The variable M approach based on any one of the methods given in previous Sections can also be used.

Pickett plot in a fractured reservoir

In the Pickett plot shown above, lines for M = 2.0 and M = 1.4 are drawn. It is clear that M varies between about 1.0 and 2.4. M can be calculated for each data point and used in the saturation equation.