|
 Water saturation fron
Simandoux Model
Water saturation fron
Simandoux Model
The response equation for the resistivity log follows the classical
form also, but it must be linearized, so the result does not often
look similar to the usual response equation. To linearize it,
porosity is replaced by (1 - Vsh) * Sw/F, and the equation is
set up in terms of conductivity instead of resistivity.
This
guarantees that the response falls back to the Archie equation
when Vsh = 0.0. Thus:
1:
COND = Sw / F * Sw * CONDw * (1 - Vsh) (water term)
+ Sw / F * (1 - Sw) * CONDh * (1 - Vsh) (hydrocarbon term)
+ Sw / Fsh * CONDsh (shale term)
+ (1 - Vsh - PHIe) * Sum (Vi * CONDi) (matrix term)
Where:
CONDh = log reading in 100% hydrocarbon
CONDi = log reading in 100% of the ith component of matrix rock
COND = log reading
CONDsh = log reading in 100% shale
CONDw = log reading in 100% water
F = formation factor of clean rock (fractional)
Fsh = formation factor of shale (fractional)
Sw = water saturation in un-invaded zone (fractional)
Vi = volume of ith component of matrix rock
Vsh = volume of shale (fractional)
CONDh
and CONDi both equal 0.0 so these two terms disappear. 1/F is
equal to (PHIe^M)/A, CONDsh equals 1/ RSH, and CONDw is equal
to 1/RW@FT. For the Simandoux equation, 1/Fsh is set equal to
Vsh/2. Various authors have proposed other assumptions for the
term 1/Fsh, so several forms of this equation are in use.
This
gives:
2 / RESD = (PHIe ^ M) / (A * RW@FT} * (1 - Vsh) * Sw ^ N
+ Vsh
/ (2 * RSH) * Sw
When
N = 2.0, this can be solved for Sw by using the standard quadratic
equation solution.
The
first term is the standard Archie equation for the non-shale portion
of the matrix, and the second term is a correction factor for
the shale fraction. The Simandoux equation is one of the most
popular and successful equations in common use which includes
a shale correction for the saturation calculation.
 Calculating simandoux Water saturation
Calculating simandoux Water saturation
3:
IF PHIe > 0.0
4: THEN C = (1 - Vsh) * A * (RW@FT) / (PHIe ^ M)
5: D = C * Vsh / (2 * RSH)
6: E = C / RESD
7: Sws = ((D ^ 2 + E) ^ 0.5 - D) ^ (2 / N)
8: OTHERWISE Sws = 1.0
Where:
A = tortuosity exponent (fractional)
C = intermediate term in Simandoux equation
D = intermediate term in Simandoux equation
E = intermediate term in Simandoux equation
M = cementation exponent (fractional)
N = saturation exponent (fractional)
PHIe = effective porosity from any method (fractional)
RESD = deep resistivity log reading (ohm-m)
RSH = resistivity of shale (ohm-m)
RW@FT = water resistivity at formation temperature (ohm-m)
Sws = water saturation from Simandoux method (fractional)
Vsh = shale content (fractional)
 COMMENTS:
COMMENTS:
References:
1. Simandoux, P., 1963, Dielectric measurements in porous
media and application to shaly formation: Revue de L’Institut
Français du Pétrole, v. 18, Supplementary Issue, p. 193–215.
2. Evaluation of Water Saturation in Shaly Formations
A. Poupon, J. Leveaux, SPWLA, 1971.
There are various versions of the Simandouc equation: the
original, modified , and Indonesian. For a clear review of
these, click HERE.
For other variations, see Schlumberger Log Interpretation
Principals / Applications, pages 8-15 and 8-16, 1989. Page
numbers may vary in other editions.
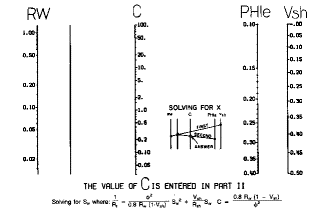
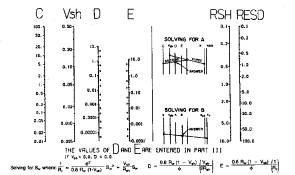
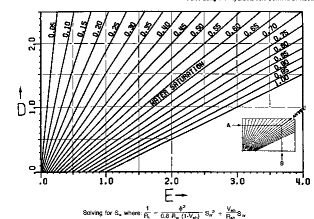
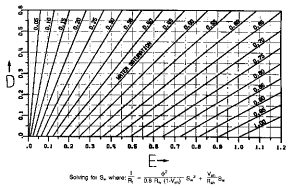
The Simandoux equation requires a three chart solution, given
below. Because of their complexity,
charts are not recommended.
|
|
|
|
Nomographs for solving Simandoux equation |
There
are many variations of the Simandoux equation. This version seems
to work well in all areas of the world; in all environments.
 RECOMMENDED
PARAMETERS:
RECOMMENDED
PARAMETERS:
RSH Range = 1.0 to 20.0 Default = 4.0
for
carbonates A = 1.00
M = 2.00
N = 2.00 (Archie Equation as first published)
for sandstone A = 0.62
M = 2.15
N = 2.00 (Humble Equation)
A = 0.81 M = 2.00 N = 2.00 (Tixier Equation -
simplified version of Humble Equation)
Asquith (1980 page 67) quoted other authors, giving values for A
and M, with N = 2.0, showing the wide range of possible values:
Average sands A = 1.45 M = 1.54
Shaly sands
A = 1.65 M = 1.33
Calcareous sands
A = 1.45 M = 1.70
Carbonates
A = 0.85 M = 2.14
Pliocene sands S.Cal. A = 2.45 M = 1.08
Miocene LA/TX
A = 1.97 M = 1.29
Clean granular
A = 1.00 M = 2.05 - PHIe
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
1. Since Sands A, B and C are 100% clean, the saturation from
Simandoux will be the same as for the Archie method. For Sand
D:
RSH = 4.0 ohm-m
PHIe = 0.11
RESD = 1.0 ohm-m
A = 0.62
M = 2.15
N = 2.00
RW@FT = 0.015 ohm-m
C = (1 - 0.33) * 0.62 * 0.015 / (0.11 ^ 2.15) = 0.717
D = 0.717 * 0.33 / (2 * 4.0) = 0.0296
E = 0.717 / 1.0 = 0.717
Sws = ((0.0296 ^ 2 + 0.717) ^ 0.5 - 0.0296) ^ (2 / 2.0) = 0.81
This
compares with an Sw of 1.03 for the Archie method.
|