|
 Water Saturation From SIGMA and FNXS Logs
Water Saturation From SIGMA and FNXS Logs
Logs that come under this designation are the Thermal Decay Time (TDT) or Neutron Lifetime (NLL)
Logs. They are also called
Pulsed Neutron (PNL) or Pulsed Decay Time (PDK) Logs. The
primary measurement is the formation capture cross section
ISIGMA). Some tools provided a compensated neutron porosity
(TPHI) derived from the ratio of the near to far detector
count rates.
Newer induced gamma ray spectroscopy tools also provide
SIGMA and TPHI, and a recent tool gives a new measurement
called fast neutron cross section (FNXS).
Both SIGMA and FNXS can be transformed into water
saturation.
On
very old logs, the primary derived value from the pulsed neutron
device is the neutron decay time (TAU), for Schlumberger logs
and the Neutron Half Life (LIFE) for Dresser logs. These are related
to the formation capture cross section (SIGMA), by the following
equation:
1:
SIGMA = 4550 / TAU for the Schlumberger tool
2:
SIGMA = 3150 / LIFE for the Dresser tool
On
modern logs, and many older ones, the SIGMA curve is displayed
and the above calculation is not needed.
 Water Saturation from TDT log.
Water Saturation from TDT log.
Here is the log response equation for
the SIGMA measurement with only hydrocarbon and water in the porosity:
3: SIGMA= PHIe * Sw * SIGw (water term)
+ PHIe * (1 - Sw) * SIGh (hydrocarbon term)
+ Vsh * SIGsh (shale term)
+ (1 - Vsh - PHIe) * Sum (Vi * SIGi) (matrix
term)
Where:
SIGh = log reading in 100% hydrocarbon
SIGi = log reading in 100% of the ith component of matrix rock
SIGMA = log reading
SIGsh = log reading in 100% shale
SIGw = log reading in 100% water
PHIe = effective porosity (fractional)
Sw = water saturation in reservoir (fractional)
Vi = volume of ith component of matrix rock
Vsh = volume of shale (fractional)
This equation is solved for Sw by assuming all other variables are
known or previously calculated:
4: SIGw = 22.0 + 0.000404 * WS(ppm)
5: SIGm = Sum (Vi * SIGi)
6: PHIe = TPHI from log if available
and no gas OR from
open hole logs
7: SWtdt = ((SIGMA - SIGm) - PHIe * (SIGh – SIGm) - Vsh * (SIGsh
- SIGm))
/ (PHIe * (SIGw - SIGh))
Solving the fast neutron response equation with CO2 instead o
hydrocarbon gives:
8: FNXSm, = Sum (Vi * FNXSi)
9: SWfnxs = ((FNXS-FNXSm)-PHIe*(FNXSco2-FNXSm)-Vsh*(FNXSsh-FNXSm))
/ (PHIe * (FNXSw - FNXSco2))
 NUMERICAL
EXAMPLE:
NUMERICAL
EXAMPLE:
1. Assume data as follows:
PHIe = 0.28
SIGw = 84 cu
SIGm = 10 cu
SIGh = 22 cu
SIGMA = 25.5 cu
Vsh = 0.20
SIGsh = 37 cu
SWtdt = ((25.5 - 10) - 0.28 * (10 - 22) - 0.20 * (37 - 10)) /
(0.28 * (84 - 22)) = 0.392.
If zone contained gas:
SIGh = 9 cu
SWtdt = ((25.5 - 10) - 0.28 * (10 - 9) - 0.20 * (37 - 10)) / (0.28
* (84 - 9)) = 0.49
 Porosity
from TDT LOGS Porosity
from TDT LOGS
In
the case of the dual detector devices, porosity from the TDT log
(TPHI or PHItdt) is calculated from the ratio of the near and far
count rate. This is the
same approach that is used for the open hole compensated neutron
log (CNL). Like the CNL, gas effects
must be taken into account.
 Limits to use of OLDER tdt for saturation calculations
Limits to use of OLDER tdt for saturation calculations
The
capture cross section is relatively inaccurate in low salinity,
low porosity situations. The chart shown below is used to
determine under what conditions the log can be used. The C/O
curve on modern tools often helps locate hydrocarbon zones in
fresher water situations.
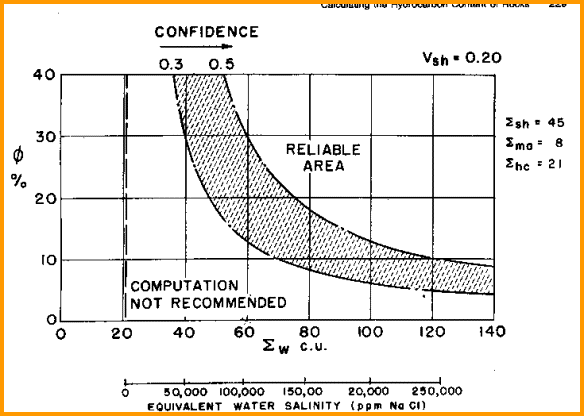
Find useful range of TDT log here
To
overcome this inaccuracy problem, older logs were run in multiple
passes and the SIGMA curves summed to reduce statistics. Typically,
five runs were summed. More modern tools have better signal to
noise ratio and do not need multiple passes. However, saturation
may still be inaccurate when salinity is less than 50,000 ppm.
Check with the service company for useful salinity / porosity
ranges on current tools as specifications are constantly changing
The
current Schlumberger tool is called the Reservoir Saturation Tool
(RST) and the term TDT may disappear as newer tools replace older
ones.
 RECOMMENDED Parameters - 2015 LIST
RECOMMENDED Parameters - 2015 LIST
|
Material |
Sigma
(c.u.) |
TPHI |
FNXS (1/m) |
|
Quartz |
4.55 |
–0.03 |
6.84 |
|
Calcite |
7.08 |
0.00 |
7.51 |
|
Dolomite |
4.70 |
0.03 |
8.51 |
|
Orthoclase |
15.82 |
–0.05 |
6.33 |
|
Albite |
7.65 |
–0.04 |
6.69 |
|
Anhydrite |
12.45 |
–0.03 |
7.14 |
|
Pyrite |
90.53 |
0.01 |
6.60 |
|
Bituminous Coal |
15.79 |
0.68 |
7.72 |
|
Dry
Illite |
20.79a |
0.22 |
8.06 |
|
Wet
Illite |
21.00
a |
0.34 |
8.02 |
|
Dry
Smectite |
14.36
a |
0.29 |
8.36 |
|
Wet
Smectite |
19.23
a |
0.68 |
8.60 |
|
Water |
22.20 |
1.00 |
7.80 |
|
Kerogen
(CH 1.3g/cm3) |
20.18 |
0.98 |
9.07 |
|
CH4
(0.05 g/cm3) |
2.50 |
–0.05 |
0.67 |
|
CH4
(0.15 g/cm3) |
7.50 |
0.21 |
2.01 |
|
CH4
(0.25 g/cm3) |
12.50 |
0.47 |
3.36 |
|
Oil
(C3H8
0.5g/cm3) |
18.21 |
0.78 |
5.44 |
|
Oil
(C3H8
0.6g/cm3) |
21.85 |
0.97 |
6.53 |
|
Diesel
(CH1.8
0.89 g/cm3) |
23.30 |
1.08 |
7.98 |
|
CO2
(0.6 g/cm3) |
0.03 |
–0.12 |
2.24 |
|
Water 0 ppm |
22.2 |
1.00 |
7.800 |
|
Water 200,000 ppm |
97.2 |
0.90 |
7.36 |
 Parameters
- 1982 LIST Parameters
- 1982 LIST
Some good legacy data
here from early sources.
SIGMAwater (SIGW)
is best derived from water salinity, which in turn can be
derived from water resistivity:
10: WS = 400000 / FT1 / ((RW@ET) ^ 1.14)
11:
SIGw = 22.0 + 0.000404 * WS
Where:
BHT = bottom hole temperature (degrees Fahrenheit or Celsius)
BHTDEP = depth at which BHT was measured (feet or meters)
DEPTH = mid-point depth of reservoir (feet or meters)
FT = formation temperature (degrees Fahrenheit or
Celsius)
FT1 = formation temperature (degrees Fahrenheit)
RW@FT = water resistivity at formation temperatures (ohm-m)
SUFT = surface temperature (degrees Fahrenheit or Celsius)
WS = water salinity (ppm NcCl)
SIGMA for hydrocarbon
(SIGh)
ranges between 0 and 23, with a default of 22 cu for typical
oil and 9 cu for gas. See graphs below.
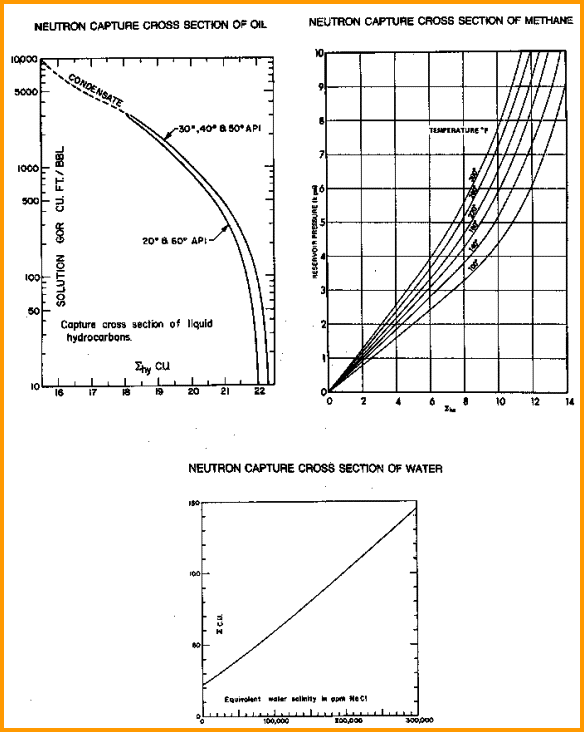
SIGMA values for oil, gas, and water
SIGMA values for shale
(SIGsh) ranges between 20 and 45. You can look at a depth plot of
your log, find the nearest, fairly thick, shale as observed on
the gamma ray log and read the average of the SIGMA curve over
the same interval. If GR is not a good shale indicator, try density
neutron separation or shallow resistivity
A
crossplot of GR vs SIGMA will do the same thing (as long as radioactivity
is a function of shale minerals and not uranium). Find the cluster
of high GR values representing shale and pick the corresponding
SIGMA shale.
SIGMA for matrix rock (SIGm)
can be taken from chartbook tables or can be calculated from the
SIGMA log curve if porosity is known from conventional log
analysis. The values in the chartbook
tables do not work well because real rocks are not pure minerals.
A method for finding SIGMAM from the log data itself uses the
following equation:
9. SIGm = (SIGMA - PHIe * SIGw) / (1 - PHIe)
This
eliminates the salt in the water in the porosity (SIGMA salt =
770) and accounts for any other minerals in the sandstone (for
example an iron rich cement where SIGMA iron = 220). Most real
rocks have SIGMA larger than the values in the tables in chartbooks.
You can vary SIGMA matrix point by point or take an average of
several calculated values.
Where:
SIGm = capture cross section of matrix (capture units)
SIGMA = capture cross section log reading (capture units)
SIGw = capture cross section of water (capture units)
PHIe = effective porosity (fractional)
This
should be done in a clean porous interval containing water.
 MATRIX PARAMETERS FOR PURE MINERALS
MATRIX PARAMETERS FOR PURE MINERALS
Caution: these values are for pure minerals and values for real
rocks are often higher.
| MINERAL |
SIGm |
| Quartz
SiO2 |
4.3 |
| Calcite
CaCO3 |
7.3 |
| Dolomite
CaCO3.MgCO3 |
4.8 |
| Feldspars |
|
| Albite
NaALSi3O8 |
7.6 |
| Anorthite
CaALSi2O8 |
7.4 |
| Orthoclase
KAlSi3O8 |
15.0 |
| Evaporites |
|
| Anhydrite
CaSO4 |
13.0 |
| Gypsum
CaSO4.2H2O |
19.0 |
| Halite
NaCl |
770 |
| Sylvite
KCl |
580 |
| Carnallite
KCl.MgCl2.6H2O |
370 |
| Borax
Na2B4O7.10H2O |
9000 |
| Kermite
Na2B4O7.4H2O |
10500 |
| Coal |
|
| Lignite |
30
+/-5 |
| Bituminous
coal |
35
+/-| |
| Anthracite |
22
+/-5 |
| Iron-Bearing
Minerals |
|
| Iron
Fe |
220 |
| Geothite
FeO(OH) |
89.0 |
| Hematite
Fe2O3 |
104 |
| Magnetite
Fe3O4 |
107 |
| Limonite
FeO(OH).3H2O |
80.0 |
| Pyrite
FeS2 |
90.0 |
| Siderite
FeCO3 |
52.0 |
| Iron-Potassium
Bearing Minerals |
|
| Glauconite
(green sands) |
25
+/-5 |
| Chlorite |
25
+/-15 |
| Mica
(Biotite) |
35
+/-1 |
| Illite
Shale |
37
+/-5 |
| Others |
|
| Pyrolusite
MnO2 |
440 |
| Manganite
MnO(OH) |
400 |
| Cinnabar
HgS |
7800 |
| |
|

