CORE POROSITY BASICS
Porosity is an intrinsic property of reservoir rocks and indicates the storage capacity of the reservoir. It is used as a primary indicator of reservoir quality, and along with a few other factors, to calculate hydrocarbon volume in place, and recoverable reserves. Petrophysicists use core porosity values to help calibrate porosity derived from well log data.

CORE POROSITY  DEFINITIONS
Porosity is the volume of the portion of the rock filled with fluids, divided by the total volume of the rock. It is usually abbreviated with Greek letter PHI, with subscripts to indicate the porosity type, eg. PHIt, PHIe, PHIsec.

Primary porosity is the porosity developed by the original sedimentation process by which the rock was created. In reports, it is often referred to in terms of percentages, while in calculations it is always a decimal fraction.

Secondary porosity is created by processes other than primary cementation and compaction of the sediments. An example of secondary porosity can be found in the solution of limestone or dolomite by ground waters, a process which creates vugs or caverns. Fracturing also creates secondary porosity. Dolomitization results in the shrinking of solid rock volume as the material transforms from calcite to dolomite, giving a corresponding increase in porosity.

In the laboratory, porosity is usually derived from easily made measurements such as weight and volume. Here are the definitions needed:

*  Vg = grain volume
*  Vp = pore volume
*  Vb = bulk volume of a rock = Vg + Vp

*  PHIcore = core porosity = Vp / Vb 
OR:
*  PHIcore = = core porosity = (Vb - Vg) / Vb

Notes:
"V" in this Chapter stands for Volume, not Velocity.
These volumes are usually reported in cubic centimeters (cc).
PHIcore may be close to total porosity (PHIt) or effective porosity (PHIe) or somewhere in-between, depending on the core analysis method and the details of how that method was applied.

The properties Vb, Vg, and Vp can be measured in the lab on full diameter core or on smaller core plugs drilled from the whole core, or from sidewall percussion or sidewall rotary cores. Whole core is best in heterogeneous reservoirs and in low porosity reservoirs.

MEASURING BULK VOLUME (Vb)
There are 3 ways to measure bulk volume:
      s. direct measurement of the dimensions of a regular solid
      b. fluid displacement using Archimedes Principle
      c. fluid displacement using calibrated container (pycmometer)

DIRECT MEASUREMENT:  Bulk Volume = Pi * Length * Radius squared
        4: Vb = PI * L * D^2 / 4

This method is less accurate due to the roughness of the surfaces of the solid and imperfections in shape.

ARCHIMEDES METHOD
This technique utilizes the Archimedes’ principle of mass displacement in a liquid (buoyancy):
        a. The core is first cleaned, dried, and weighed in air (WTdry)
        b. The core sample is then saturated with a wetting fluid and weighed (WTsat)
                 (the core may be coated with paraffin to prevent evaporation)
        c. The sample is then submerged in the same fluid and its submerged weight is measured (WTsub)
        d. The bulk volume is the difference between the last two weights divided by the density of the fluid.
        e. The porosity  is the difference between the first two weights divided by the density of the fluid.

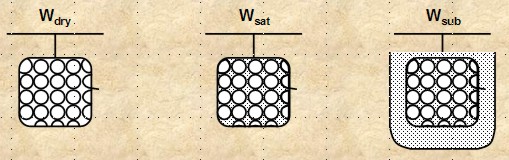
Bulk Volume = (Weight in air (saturated) - Weight submerged) / Density of Fluid
        5: Vb = (WTair - WTsub) / DENSfl
        6: Vg = (WTdry - WTsub) / DENSfl
        7: Vp = (WTsat - WTdry) / DENSfl
        8: PHIt = (WTsat - WTdry) / (WTsat - WTsub) = Vp / Vb

Bulk Density = Saturated Weight / Bulk Volume
        9: BulkDens = WTsat / Vb

If clays are present and sample is maintained at a high humidity (not over dried), this last equation gives PHIe, not PHIt.

Laboratory measurements using this technique are very accurate.

CALIBRATED DISPLACEMENT METHOD
The bulk volume can be determined also by the volume of the displaced fluid. Fluids that are normally used are  water, which can easily be evaporated afterwards, and mercury, which normally does not enter the pore space in a core sample due to its non-wetting capability and its large interfacial tension against air.

Bulk Volume = Volume of Displaced Fluid = Weight Displaced Fluid / Density Displaced Fluid
       10: Vb = WTdisp / DENSfl

Laboratory measurements using this technique are very accurate.

  NUMERICAL EXAMPLE:
    WTdry = dry weight in air = 16.0 gm
    WTsat = weight of saturated sample in air = 20.0 gm
    WTcoated = weight of dry sample coated with paraffin = 20.9 gm (density of paraffin = 0.9 gm/cc)
    WTsub = weight coated sample immersed in water at 70 °F = 10 gm (density of water = 1.0 gm/cc)
Determine bulk volume
      Weight of paraffin = WTcoated - WTsar = 20.9 - 20.0 = 0.9 gm
      Density of Parrafin = 0.9 gm/cc
      Volume of paraffin = WTpar / DENSpar = 0.9 / 0.9 = 1.0 cc
      Weight of water displaced = WTcoated - Wtsub = 20.9 - 10.0 = 10.9 gm
      Volume of water displaced = 10.9 / 1.0 = 10.9 cc
      Volume of water minus displaced-volume of paraffin = 10.9 - 1.0 = 9.9 cc
      Bulk volume of rock = 9.9 cc

 MEASURING GRAIN VOLUME (Vg)
There are 3 ways to measure grain density in the lab:
        a. assume a grain density, compare to dry weight
        b. displaced fluid method
        c. Boyle's Law

ASSUMED GRAIN DENSITY
Determine Vg from the dry weight of the sample and the rock grain density (2.65 gm/cc for quartz grains). This method is not very accurate if grain density varies due to varying mineralogy.

Grain Volume = Dry Sample Weight / Grain Density
        11: Vg = WTdry / DENSMA

DISPLACED FLUID METHOD
A more accurate approach is to use the displaced fluid volume. First the core plug is measured to obtain its bulk volume, as described earlier  Then the sample is crushed to eliminate all porosity and weighed (WTgr). A glass tube filled with water, called a pycnometer to confuse novices, is weighed (W1), then the crushed rock is placed in the tube (still filled with water), and weighed again WT2). The difference in weights gives the volume of displaced fluid.

Displaced Volume = Crushed Sample Weight + Water-filled tube Weight  - Combined Weight
        12: Vdisp = (WT2 - WT1)

Grain Volume = Displaced Volume / Water Density
        13: Vg = Vdisp / DENSwater

Porosity = (Bulk Volume - Grain Volume) / Bulk Volume
        14: PHIt = (Vb - Vg) ' Vb

If clays are present and sample is maintained at a high humidity (not over dried), this last equation gives PHIe, not PHIt.

Grain Density = Dry Weight in Air / Grain Volume
        15: GrainDens = WTdry / Vg

NUMERICAL EXAMPLE:
    WTdry = Weight of dry crushed sample in air = 16.0 gm,
    WT1 = Weight of pycnometer filled with water at 70 °F =  65.0 gm
    WT2 = Weight of pycnometer filled with water and crushed sample = 75.0 gm
Calculate grain volume
    Volume of water displaced = 16.0 + 65.0 - 75.0 = 6.0 gm
    Grain Volume = 6.0 / 1.0 = 6.0 cc
Calculate porosity
    Bulk volume of the sample = 9.9 cc, from previous example
    Total porosity = (9.9 - 6.0) / 9.9 = 0.394 fractional porosity (39.4%)

BOYLE'S LAW METHOD
An alternate grain volume method makes use of Boyle’s Law.

This gas transfer technique involves the injection and decompression of gas (Helium, CO2, or N2) into the pores of a fluid-free (vacuum), dry core sample. Either the pore volume or the grain volume can be determined, depending upon the instrumentation and procedures.

To determine grain volume using ideal gas law at constant temperature:
   a. connect two cells of known volume, Vcell1 and Vcell2
   b. close valve between cells, apply pressure P1 to cell 1
   c. place dry core sample in cell 2, seal and evacuate cell 2 
   d. open valve and measure pressure P2

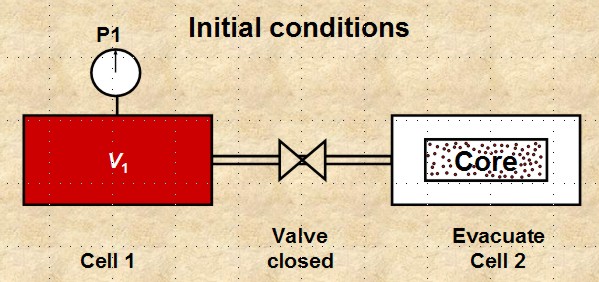
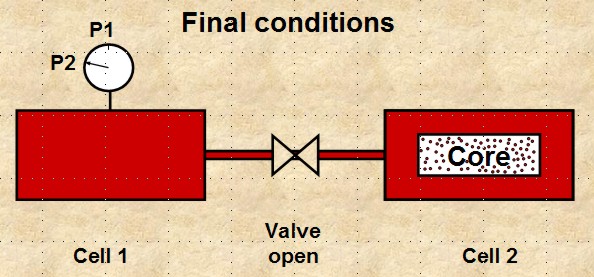
Boyle's Law apparatus to measure grain volume Vg

          16: V2 =  P1 * Vcell1 / P2
Since V2 = Vcell1 + Vcell2 - Vg And Vtotal = Vcell1 + Vcell2
Then  17: Vg = Vt - Vf
 

MEASURING PORE VOLUME
In previous sections pore volume Vp was derived from volumetric methods based on weight and density. Semi-direct measurement of porosity can also be attempted.
 

BOYLE'S LAW METHOD
Pore volume measurements can be done by using the Boyle’s Law model, where the sample is placed in a rubber sleeve holder that has no void space around the periphery of the core and on the ends. Such a holder is called the Hassler holder, or a hydrostatic load cell. Helium or one of its substitutes is injected into the core plug through the end stem.

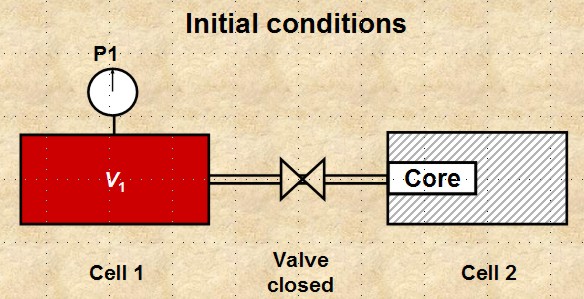
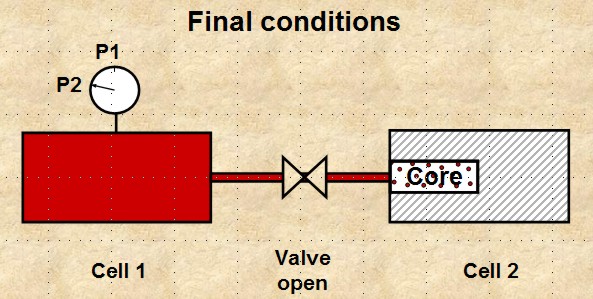
Boyle's Law apparatus for determining porosity

          18: V2 =  P1 * Vcell1 / P2
Since V2 = Vcell1 + PHIe
Then  19: Vp = V2 - Vcell1
 

 FLUID SUMMATIONS METHOD
This technique is used to measure the volume of gas, oil and water present in the pore space of a fresh or preserved (peel-sealed) core of known bulk volume. The volumes of the extracted oil, gas, and water are added to obtain the pore volume and hence the core porosity.

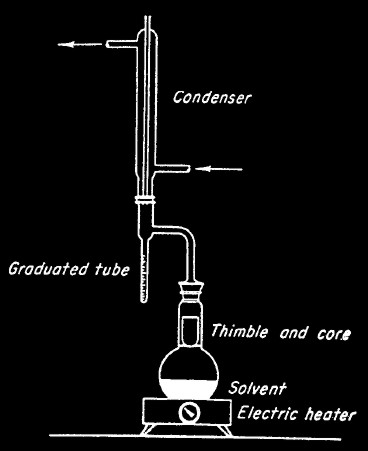
DEAN-STARK CORE ANALYSIS METHOD
This method is used in poorly consolidated rocks such as tar samds and involves disaggregating the samples and weighing their constituent components. Samples are usually frozen or wrapped in plastic to preserve the contents during transport. In the lab, the still frozen cores are slabbed for photography and description, then samples are selected and weighed.

Samples are then heated and crumbled to drive off water, and weighed again. The weight loss gives the water weight. Solvents are used to remove oil or tar. The sample is weighed again and the weight loss is the weight of oil. The matrix rock is separated into clay and mineral components by flotation, dried and weighed again, giving the weight of clay and weight of the mineral grains.
      20: WTwtr = WTsample - WTheated
      21: WTtar = WTheated - WTminerals&clay

By dividing each weight by its respective density and adjusting each result for the total weight of the sample, the volume fraction of each is obtained. Porosity is the sum of water plus oil volume fractions  Because the bound water in the clay is driven off by the drying sequences, this porosity is the total porosity.
      22: VOLwtr = WTwtr / DENSwtr / WTsample
      23: VOLtar = WTtar / DENStar / WTsample
      24: PHIcore = VOLwtr + VOLtar

Dean-Stark laboratory apparatus

Assuming clay bound water is driven off by heating and drying, then PHIcore equals total porosity. From comparison to log analysis results, it appears that some clay bound water remains in many cases, so PHIcore lies between total and effective porosity from log analysis.

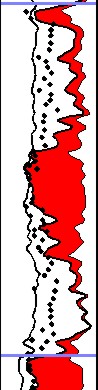
Example of Dean-Stark porosity (dots) showing that it is less than total porosity
 from logs (black curve) due to incomplete drying of clay. Trying to match log
 porosity directly to core may be futile in many cases. Scale is 0.50 to 0.00.

OIL MASS FROM CORE LISTINGS
If not provided on the core listing, the equivalent value of tar mass from core analysis is derived from porosity, oil saturation, and an assumed oil density:
     25:  Wtar = PHIcore * Star * DENStar
     26:  Wwtr =  PHIcore * Swtr * DENSwtr
     27:  Wrock = (1 – PHIcore) * GR_DENScore

Where:
  Star = tar volume relative to pore volume
  Swtr = water volume relative to pore volume
  PHIcore = volume of water + valume of tar
  Wtar = tar mass fraction
  Wwtr = water mass fraction
  Wrockcore = rock mass fraction
 

If saturations (or pore volume) are known, as well as core porosity, all other terms can be calculated. Some core analysis reports do the math for you, some do not.
 

Since GR_DENScore represents a mixture of quartz and shale, this value should vary with shale volume. However  shale volume is never reported on core analysis, so the composite grain density from the rock sample is used. If grain density is not recorded in the core analysis, we must assume a constant of  2650 kg/m3 or lower.

FLUID VOLUMES FROM CORE LISTINGS
If not provided on the core listing, the equivalent value of tar volumes from core analysis are derived from porosity, tar mass fraction, and an assumed oil density:
     27: Star = Wtar / (PHIcore * DENStar)
     28: Swtr = Wwtr / (PHIcore * DENSwtr)
OR 29: Swtr = 1.00 - Star

Where:
  Star = tar volume relative to pore volume
  Swtr = water volume relative to pore volume
  PHIcore = volume of water + valume of tar
  Wtar = tar mass fraction
  Wwtr = water mass fraction
 

If oil mass fraction and water mass fraction are known, as well as core porosity, all other terms can be calculated. Some core analysis reports do the math for you, some do not.

POROSITY FROM MICRO CT SCANS
Porosity is directly calculated from high resolution digital images such as those shown below. This calculation is the ratio of the number of voxels that fall into the pore space (black and dark-gray) to the total number of voxels in a 3D image. The task of separating the pores from grains in such 3D objects is called image segmentation.  The main technical challenge in image segmentation is the gradual transition from dark to light shade of gray at the edges of the pore space. Proprietary image-processing algorithms are used, which   include statistical analysis of the gray-scale images. As a result, the pore space is accurately separated from the mineral matrix and the porosity is computed. Source: www.ingrainrocks.com.
 

   
    Clean sand 39%                            Tight sand 5%                 Poorly sorted 12%            Silty Shale 8%
                                Black = Porosity,  Grey = Matrix Grains,  White = Heavy Minerals

SAMPLE CORE ANALYSIS REPORT

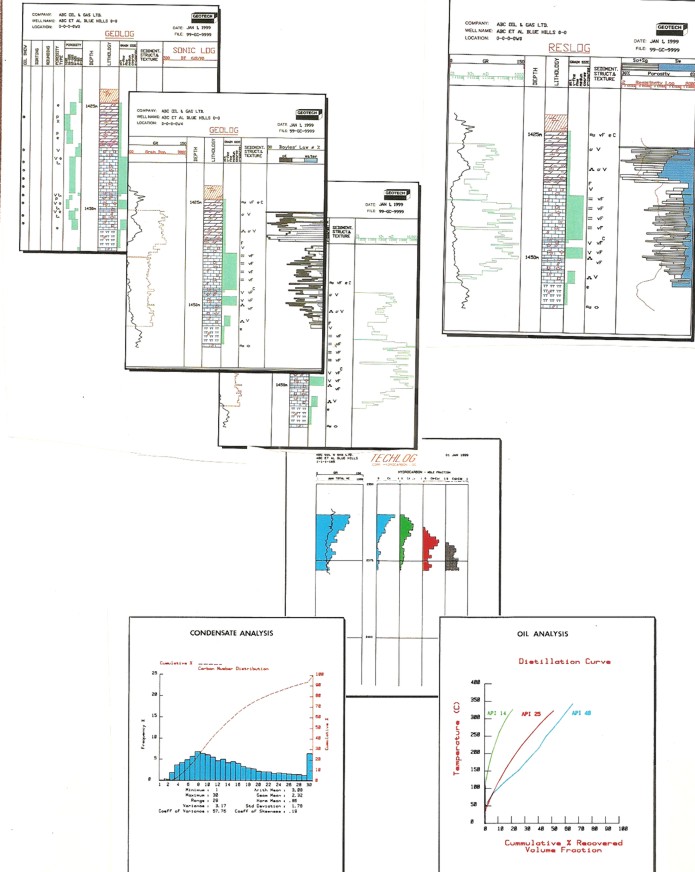
Samples of core analysis and core description plots, with a few of the posible histograms and crossplots that can be made.