|
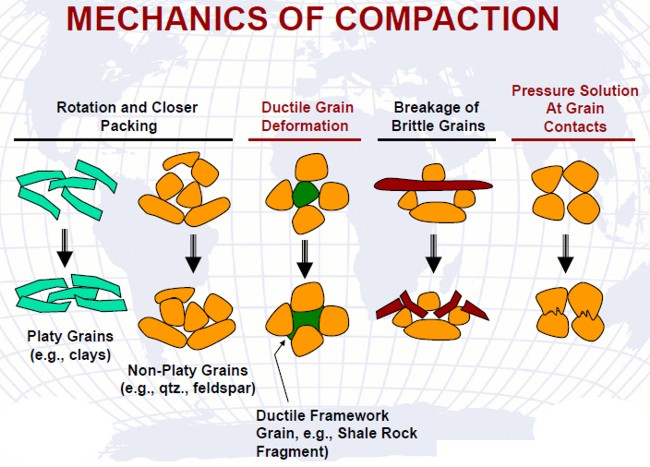
Normal sedimentary processes of compaction compress the rocks, reducing porosity and sometimes changing the shape and size of rock grains, as shown in the illustration above. The pressure difference between overburden and internal pore pressure is referred to as the effective overburden pressure. During pressure depletion (oil or gas production) operations, the internal pore pressure decreases and, therefore, the effective overburden pressure increases. This increase causes the bulk volume of the reservoir rock to reduce, and the rock grains to expand, reducing porosity.
Compressibility is the relative
volume change of matter per unit pressure change under conditions of
constant temperature. Usually, petroleum reservoirs can be
considered isothermal (an exception: thermal stimulation such as
steam assisted gravity drainage, SAGD, or fire floods).
Increasing pressure causes volume of material to decrease
(compression). Decreasing pressure causes volume expansion.
Wjere: For some oilfield purposes, Cm and Cb are small, and the composite formation compressibility Ct is assumed to be equal to Cp. Typical values for Ct are 3 to 25 * 10^-6 psi-1. Ct varies inversely with porosity and pressure, and numerous authors have published correlations applicable to specific rock types.
The inverse of a compressibility is a bulk modulus, for example
Kc = 1 / Ct is the composite bulk modulus of the porous rock.
Descriptive terms and abbreviations used in the literature
vary widely, for example Cr is sometimes used to represent the rock
matrix compressibility Cm, and the rock matrix is sometimes referred
to as the "empty rock frame".
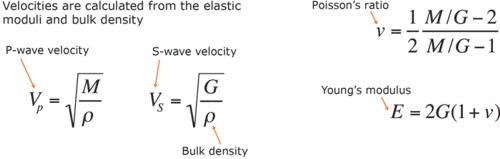
The application of stresses to the faces of the sample generates strains in the rock frame that are computed locally using the finite element method (FEM). The resulting effective deformations of the sample are related to the stresses applied at the boundaries to calculate the effective elastic moduli. This application assumes linear elasticity laws are valid within the sample. Therefore, the elastic moduli can be converted into the elastic-wave velocities.
Various
loading configurations are applied to
the same digital sample to obtain the
effective elastic moduli (e.g., the bulk
and shear). Source:
www.ingrainrocks.com.
|
||
|
Page Views ---- Since 01 Jan 2015
Copyright 2023 by Accessible Petrophysics Ltd. CPH Logo, "CPH", "CPH Gold Member", "CPH Platinum Member", "Crain's Rules", "Meta/Log", "Computer-Ready-Math", "Petro/Fusion Scripts" are Trademarks of the Author |
||


|
||
| Site Navigation | LAB TECH MEASURING COMPRESSIBILITY OF ROCKS | Quick Links |

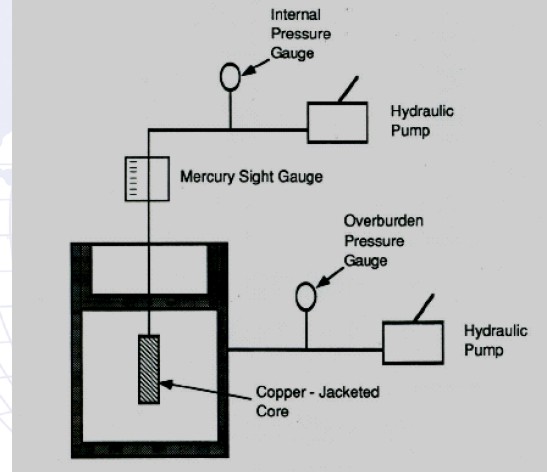
 Processing
of micro CT scans to determine
elastic moduli is done by by simulating a static deformation
experiment on a 3D digital rock sample. These tests are
nondestructive and can be run on small samples such as drill
cuttings.
Processing
of micro CT scans to determine
elastic moduli is done by by simulating a static deformation
experiment on a 3D digital rock sample. These tests are
nondestructive and can be run on small samples such as drill
cuttings.