|
Stage
1: Preparation for
drainage -
core saturated with wetting
phase.
Stage
2: Irreducible wetting phase (drainage) -
inject non-wetting
phase until steady state, measure saturation,
no wetting phase
will be produced after steady state.
Stages 3-6:
Inject wetting phase
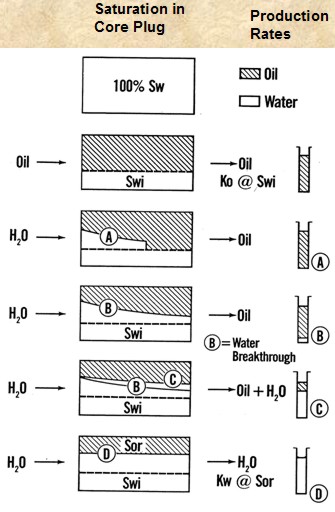
Stage 3: (A) Wetting phase has not yet reached outflow
face,
only
nonwetting phase produced at outflow face.
Stage 4: (B) Wetting phase just reaches outflow face,
called breakthrough,
wetting
phase will be produced at outflow face.
Stage 5: (C) As injection of wetting phase
continues, production of nonwetting phase
decreases (unsteady state).
Important
to take many data points during this decrease (»cummulative
nonwetting phase produced
»and
production rate for both phases).
Stage 6:
(D) Eventually, no more nonwetting phase
is produced, allowing residual nonwetting phase saturation to be
determined.
immiscible displacement
incompressible fluids
linear, 1-D flow
capillary pressure neglected
cumulative
nonwetting phase production,
Determine relative permeability
ratio from fractional flow
(production rate measured at
outflow face):
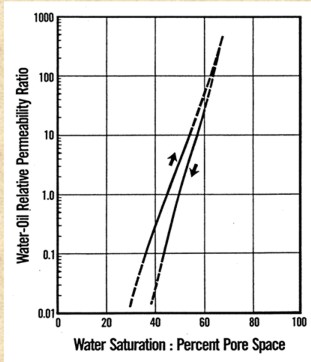
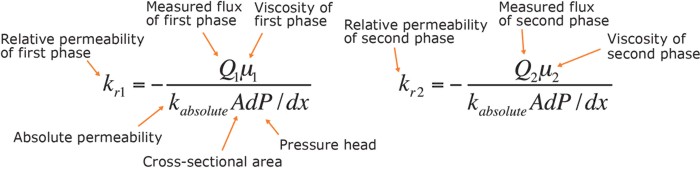
4: Qtotal = Qwet + Qnonwet 5: Fwet = Qwet / Qtotal Relative permeability ratio Fwet is related to relative permeability by the equation: 6: Fwet = 1 / (1 + (Kr_nonwet / Kr_wet) * (MUwet / MUnonwet)) It is obvious from the above that one of Kr_nonwet or Kr_wet must be determined independently in order to find the other, using Fwet. This is done with correlation equations based on capillary pressure curves. The process
starts with calculation of
effective water saturation (not
to be confused with any form of
water saturation from log
analysis). Pretty messy but so is the math for the lab method.
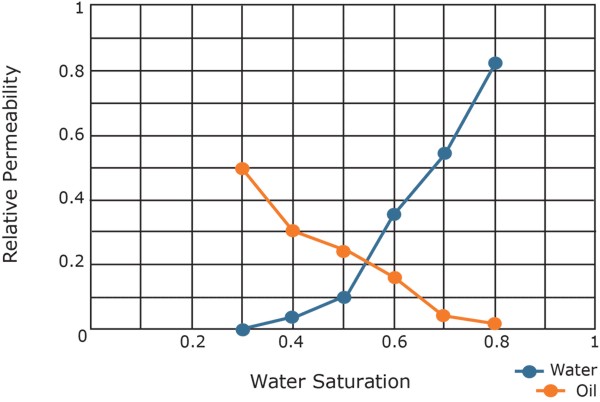
If a single fluid is present in a rock, its relative permeability is 1.0. Relative permeability allows comparison of the different abilities of fluids to flow in the presence of each other, since the presence of more than one fluid generally inhibits flow.
Key parameters that affect relative permeability include:
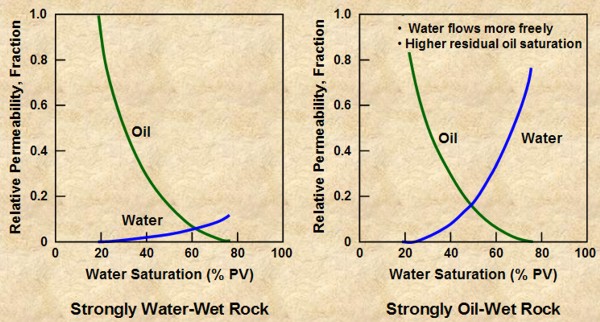
These parameters define the wetting (or contact) angles, which are formed at an interface between fluid and mineral. A wetting angle is larger than 90 degrees if the fluid is wetting and smaller than 90 degrees if the fluid is non-wetting.
The slow multiphase viscous flow needed for relative permeability estimates is simulated using the lattice Boltzmann method (LBM). LBM mathematically mimics the equations of multiphase viscous flow by treating the fluid as a set of particles with certain interaction rules between the particles belonging to the same fluid, different fluids, and the fluids and pore walls. LBM directly simulates static and dynamic configurations of the contacts between the fluid phases and the pore walls by taking into account surface tension and contact angles. It allows for the estimation of irreducible water and hydrocarbon saturations Source: www.ingrainrocks.com.
|
||
|
Page Views ---- Since 01 Jan 2015
Copyright 2023 by Accessible Petrophysics Ltd. CPH Logo, "CPH", "CPH Gold Member", "CPH Platinum Member", "Crain's Rules", "Meta/Log", "Computer-Ready-Math", "Petro/Fusion Scripts" are Trademarks of the Author |
||


|
||
| Site Navigation | LAB TECH MEASURING RELATIVE PERMEABILITY IN ROCKS | Quick Links |