|
 Porosity
From the Neutron Log Porosity
From the Neutron Log
The
neutron log is widely used to estimate porosity. The method
works well when shale volume and matrix rock neutron
response are accurately known. Errors as large as 8%
porosity can occur, and 2 to 4% are common if incorrect
assumptions are made.
If both density and neutron logs are available, a superior
model that does not require matrix rock properties is the
Shale Corrected Density Neutron
Complex Lithology Crossplot Method. The Meta/Kwik
spreadsheet for this model is available at
Downloads and Spreadsheets.
 Neutron Log RESPONSE EQUATION
Neutron Log RESPONSE EQUATION
The response equation for the neutron porosity log also follows
the classical form:
1:
PHIN = PHIe * Sxo * PHINw (water term)
+ PHIe * (1 - Sxo) * PHINh (hydrocarbon term)
+ Vsh * PHINsh (shale term)
+ (1 - Vsh - PHIe) * Sum (Vi * PHINi) (matrix term)
Where:
PHINh = log reading in 100% hydrocarbon
PHINi = log reading in 100% of the ith component of matrix rock
PHIN = log reading
PHINsh = log reading in 100% shale
PHINw = log reading in 100% water
PHIe = effective porosity (fractional)
Sxo = water saturation in invaded zone (fractional)
Vi = volume of ith component of matrix rock
Vsh = volume of shale (fractional)
 Porosity
From the Neutron Log
Porosity
From the Neutron Log
To solve for porosity from the
neutron log, we assume PHINh, PHINi,
PHINsh, PHINw, and Vsh are known. We also assume PHINw = PHINh and
Sxo = 1.0 when no gas is present. If gas is indicated, we make
assumptions about PHINh and Sxo, usually in the form of a correction
factor to the gas free case, as described later.
We usually assume PHINw = PHINh = 1.0, and that PHINsh
and Vsh are known.
Apply lithology and shale corrections:
2: PHINm = (PHIN - PHINMA) / (PHINW -
PHINMA)
3: PHInc = PHINm - Vsh * PHINSH
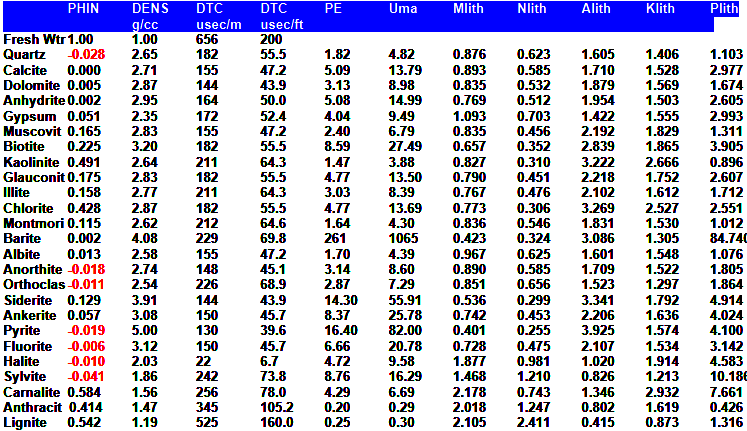
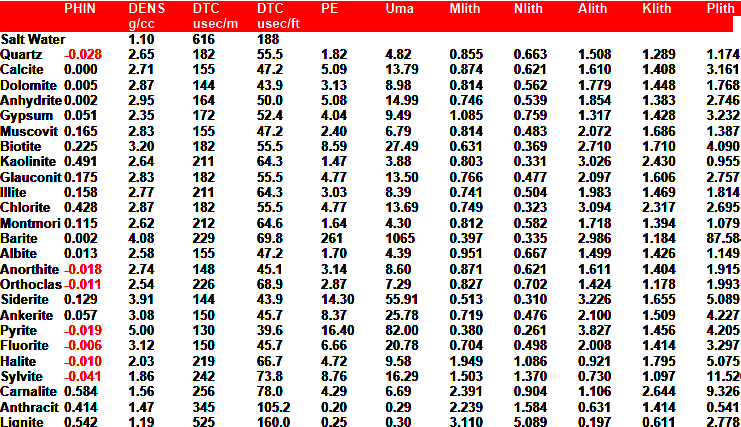
Mineral and fluid parameters are shown HERE.
Shale properties are selected from the log in an obvious shale
zone.
Compute neutron log gas correction.
4: IF NEUTRONGASSWITCH$ = "ON"
5: THEN PHIN = KN * PHIN
Where:
KN = neutron gas correction factor (fractional)
PHIN = porosity from neutron log corrected for lithology or gas
(fractional)
PHInc = porosity from neutron log corrected for shale (fractional)
PHINSH = apparent neutron log porosity of 100% shale (fractional)
Vsh = volume of shale (fractional)
 COMMENTS:
COMMENTS:
References:
1. Radioactive Well Log Interpretation
J.P. Campbell, A.B. Winter,
Lane Wells, 1946
2. Experimental Basis for Neutron Log
Interpretation
J.T. Dewan, L.A. Allard,
Petroleum Engineer, 1953
3. Sidewall Epithermal Neutron Porosity Log
J. Tittman, H. Sherman, W.A. Nagel, R.P. Alger,
JPT, 1966
4. Dual Spacing Neutron Log - CNLi
R.P. Alger, S. Locke, W.A. Nagel, H. Sherman,
AIME, 1971
A chart to solve this equation, along with the lithology shifts
can be found below.
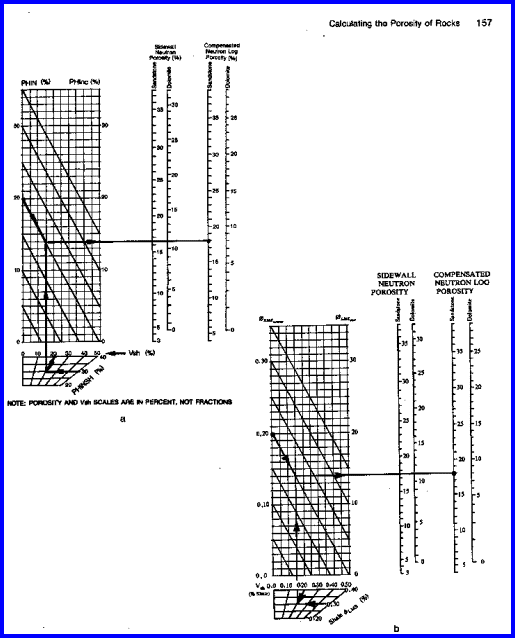
Chart for Estimating Shale Corrected Neutron Porosity
KN
is in the range of 1.0 to 3.0 depending on depth of invasion,
gas density and logging tool type. Use local experience. Apply
this correction only if gas is known to be present and log reading
is still too low after lithology corrections.
The neutron log corrected for shale is one of the least accurate
methods and should only be used if no other porosity data is available.
This is common for wells drilled prior to 1957 or for wells logged
through casing or drill pipe.
NOTE: If neutron
log is on a scale (sandstone, limestone) that does not match the
rock mineral, lithology corrections are required.
 NUMERICAL EXAMPLE:
NUMERICAL EXAMPLE:
1. Assume data from Sand "D" in Classic Example 1
PHIN = 0.28
PHINSH = 0.30
Vsh = 0.33
Neutron log type = CNL
CNL / FDC units = Sandstone
Rescaling is not required, as log is in correct units.
No gas correction is required.
PHInc = 0.28 - 0.33 * 0.30 = 0.18
 Porosity from ANCIENT Neutron Logs
Porosity from ANCIENT Neutron Logs
Old style gamma ray neutron (GRN) logs are un-scaled neutron logs
recorded in counts per second or API units. They are common in
ancient wells. The log carries a gamma ray curve (GR) in the left
hand track and a neutron curve (NEUT) in the right hand track.
No borehole or casing corrections have been applied to these logs.
Neutron log deflections to the left (lower count rate) represent
higher porosity.
A
large number of charts for specific tools, spacings, borehole
conditions and rock types were available from service companies,
such as the one shown below. These may no longer be
easily found today, and the semi-logarithmic approach described
below works well except in very low porosity .
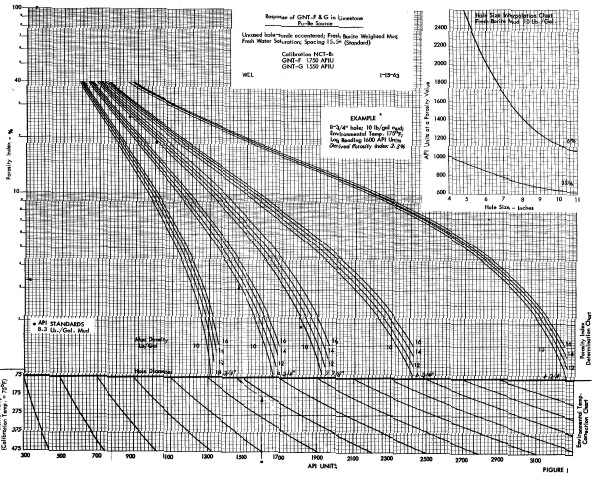
GNT-F or G neutron porosity interpretation chart. Hundreds
of such charts exist for dozens of tools for a large range of
hole sizes, mud weights, and casing sizes. most are not
contained in conventional chart books. Some are available on the
Denver Well Log Society CD set sold by
SPWLA.
There were three source types used (RaBe, PuBe, and AmBe) and
several source - detector spacings (15.5 and 18.5 inches were
common), combined with hole size, mud weight, and casing
variations, leading to a plethora of transforms. Some service
companies didn't have a lot of faith in their charts - one used
the term "Strata Index" instead of "Porosity" on the Y-axis.
If
no appropriate chart exists, or if you don't believe in them, it is expedient to use the "High
porosity- Low porosity" method. A logarithmic scale can be applied algebraically with
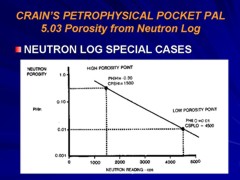
the following formulae using the high porosity/low porosity method.
Calculate slope and intercept of semi-logarithmic relationship
between neutron count rate and porosity:
1: SLOPE = (log (PHIHI / PHILO)) / (CPSHI - CPSLO)
2: INTCPT = PHIHI / 10 ^ (CPSHI * SLOPE)
Calculate total porosity:
3: PHIn = INTCPT * 10 ^ (SLOPE * NCPS)
4: PHIe = PHIn - (Vsh * PHINSH)
Where:
CPSHI = GRN counts at high porosity point (cps)
CPSLO = GRN counts at low porosity point (cps)
NCPS = neutron log reading in CPS or arbitrary units (cps)
PHIHI = high porosity point (fractional)
PHILO = low porosity point (fractional)
PHIn = apparent neutron log porosity, uncorrected for shale (fractional)
 COMMENTS:
COMMENTS:
The graphical solution to this formula is given below.
Complete gas, shale and matrix corrections will still be required
and are detailed in the following sections.
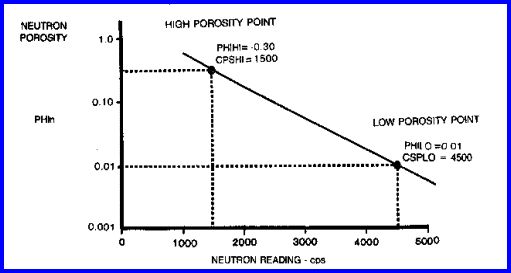
Chart for Estimating Porosity from Neutron Counts per Second -
no shale correction.
A graph like this must be made for each well to be analyzed
since the original logs were
seldom calibrated to any fixed standard.
A
large number of charts for specific tools, spacings, borehole
conditions and rock types are available from service companies.
 RECOMMENDED PARAMETERS:
RECOMMENDED PARAMETERS:
PHIHI should be in the range 0.20 to 0.35.
PHILO should be in the range 0.01 to 0.05, and cannot be zero.
 NUMERICAL EXAMPLE:
NUMERICAL EXAMPLE:
1. Assume an old GRN log where:
PHIHI = 0.30
PHILO = 0.01
NCPS = 2500 cps
CPSHI = 1500
CPSLO = 4500
SLOPE = (log (0.30 / 0.01)) / (1500 - 4500) = - 0.000492 (rounded
to - 0.0005)
INTCPT = 0.30 / 10 ^ (1500 * (-0.0005)) = 1.6432
PHIn = 1.6432 * 10 ^ (-.0005 * 2500) = 0.096
 NEUTRON
ENVIRONMENTAL CORRECTIONS
NEUTRON
ENVIRONMENTAL CORRECTIONS
Environmental corrections are based on the following equations,
taken from “Experimental Determination Of Environmental
Corrections For A Dual-Spaced Neutron Porosity Log”, by Dan M.
Arnold and Harry D. Smith, Jr., SPWLA June 1981, updated
January, 1982. These are for the Welex-Halliburton tool.
Equations for other tools will vary somewhat due to differences
in tool design and experimental error.
In open hole, borehole size corrections are normally made
automatically during
logging based on the caliper
log, For cased hole, borehole size, casing thickness, and cement
thickness corrections are made automatically, based on input
parameters. The equations for the remaining corrections are often used
in computer post-processing of the log. All porosity values and
corrections are in fractional porosity units.
Basic Porosity
Equation
1: IF NRAT <= 200
2: THEN PHIN = - 2.552 * 10^-2 + 2.513 * 10^-3 * NRAT -
0.930 * 10^-6 * NRAT^2
3: ELSE PHIN = 2.2754 - 1.980 * 10^-2 * NRAT + 5.311 *
10*-5 * NRAT^2
Where:
NRAT = ratio of short spaced to long spaced detector count rates
PHIN = raw neutron porosity before corrections (fractional)
Borehole Size
Correction
4: Kbh1 =
(CAL - 8) * (-0.0025 - 0.1063 PHIN + 0.5419 PHIN^2 - 0.6946 * PHIN^2.8)
+ (0.001445 * (CAL - 8)^2)
* PHIN
5: Kbh = MAX (Kbh1, - 0.16)
6: PHINbh = PHIN + Kbh
Where:
CAL = diameter of the borehole (inches)
Kbh = borehole size correction (fractional porosity)
PHINbh = raw neutron porosity corrected for borehole size
This correction has usually been applied at time of logging - do not
apply it again.
Equivalent Open Hole Conversion
7: PHINoh = - 0.0174 + 0.3702 * PHINbh + 2.958 *
PHINbh^2 -
4.070 * PHINbh^3 + 3.00 * PHINbh^6
This is the equivalent of limestone
porosity (PHIN_LS) before any other corrections are made and is what
we read from a compensated neutron log. Further corrections and
lithology conversion are shown below..
Mud Cake
Correction
8: Hmc = MAX (0, CAL – BITZ)
Automatic caliper compensated
9A: Kmc = (- 0.0120 - 0.061 * PHIN + 0.271 * PHIN^2) * Hmc
+ (- 0.0129 + 0.088 * PHIN - 0.154 * PHIN^2) *
Hmc^2
No caliper compensation
9B: Kmc = (-
0.0048 - 0.039 * PHIN + 0.353 * PHIN^2) * Hmc
+ (- 0.0221 + 0.107 * PHIN - 0.195 * PHIN^2) *
Hmc^2
Where:
Hmc = mud cake thickness (inches)
Kmc = mud cake correction (fractional porosity)
Formation
Salinity Correction
10: Kfs = PHIN * ( - 3.5 * 10^-4 * WS/1000 + 6.0 * 10^-7 *
(WS/1000)^2))
Where:
WS = water salinity (ppm NaCl)
Kfs = formation salinity correction (fractional porosity)
Borehole
Salinity Correction
11: Kbs.= PHIN * (
- 2.0 * 10^-4 * MS/1000 + 1.9 * 10^-6 * (MS/1000)^2))
Where:
MS = mud salinity (ppm NaCl)
Kbs = borehole salinity correction (fractional porosity)
The reference
paper uses the same salinity for both formation and borehole (MS =
WS) – this only true if invasion is fairly deep.
Mud Weight
Correction
For normal mud
12A: Kmw = PHIN * (1.04 * 10^-2 * (WM - 8) + 3.47 * 10^-4 * (WN
- 8)^2)
For barite mud
12B: Kmw = PHIN * (5.21 * 10^-3 * (WM - 8) + 8.68 * 10^-5 * (WN
- 8)^2)
Where:
WM = mud weight (pounds per gallon)
Kmw = mud weight correction (fractional porosity)
Standoff
Correction
For standoff X <= 0.5
13A: A2 = 14 * X
14A: B2 = 1.6 * X
15A: C2 = 0.05 * X
For standoff X > 0.5
13B: A2 = - 6.5 + 25 * X
14B: B2 = 1.5 - 4.6 * X
15B: C2 = - 0.08 +
0.21 * X
16: A1 = A2 + B2 * CAL + C2 * CAL^2
17: B1 = - 0.0254 + 0.06834 * PHIN - 0.08814 * PHIN^2
18: C1 = 0.0025 - 0.0081 * PHIN - 0. 00994 * PHIN^2
19: Kst =
B1* A1 + C1 * A1^2
Where:
CAL = borehole diameter (inches)
X = standoff (inches)
Kst = standoff correction (fractional porosity)
Temperature
Corrections
20: Ktc = (0.008 + 0.062
* PHIN + 0.092 * PHIN^2) * (FT – 75) / 225)
Where:
FT = borehole temperature (deg F)
Ktc = temperature correction (fractional porosity)
CASED HOLE
CORRECTIONS
Casing Thickness Correction
21: He = 0.5 * (Dcsg - (Dcsg^2 - 0.3667 *
WTcsg)^0.5)
22: Kcs = 0.171 * (0.3 - He)
Where:
He = casing thickness (inches)
Dcsg = outside diameter of casing (inches)
WTcsg = casing weight
(lb/ft)
Kcsg = casing correction (fractional porosity)
Cement
Thickness Correction
23: Hcmt = 0.5 * (CAL - Dcsg)
24: Kcmt = (1.5 - Hcmt)
* (0.020 - 0.0667 * PHIN^2)
Where:
Hcmt = cement thickness (inches)
Kcmt = temperature correction (fractional porosity)
Limestone
Porosity
Open Hole - assuming Kbs has been applied at logging time
25A: PHIN_LS = PHINoh + Kmc + Kfs + Kbs + Kmw + Kst + Ktc
Cased Hole - assuming Kbs has
been applied at logging time
25B: PHIN_LS = PHINoh + Kfs + Kbs + Kmw + Ktc + Kcsg + Kcmt
Borehole size, casing, and cement corrections are normally made
automatically during logging, DO NOT APPLY THEM AGAIN. Salinity and
temperature corrections may or may NOT have been applied while
logging. Some commercial software packages apply ALL corrections with no
options to apply only those that are needed. When in doubt, apply NO corrections.
See next
section to apply Lithology corrections.
 Matrix
Offset for Neutron Logs Matrix
Offset for Neutron Logs
It is often necessary to rescale a neutron log, which is already
in porosity units, for lithology. The final result is called
PHINm - Neutron Log Porosity Corrected
for Lithology.
For SNP tools only, mud cake thickness correction is needed first:
1: PHINmc = PHIN - 0.01 * (max (0, CAL - BITZ)
/ KX1)
Where:
BITZ = bit size (inches or mm)
CAL = caliper (inches or mm)
KX1 = 1.0 for English Units (inches)
KX1 = 25.4 for Metric Units (millimeters)
 QUICKLOOK METHODS FOR
PHINm
QUICKLOOK METHODS FOR
PHINm
Sandstone
porosity units to limestone units.
CASE 1a: PHIN_LS = PHIN_SS - 0.03
SNP Log
CASE 1b: PHIN_LS = PHIN_SS - 0.04
CNL Log
Limestone porosity units to sandstone units.
CASE 2a: PHIN_SS = PHIN_LS + 0.03
SNP Log
CASE 2b: PHIN_SS = PHIN_LS + 0.04
CNL Log
Limestone porosity units to dolomite units.
CASE 3a: PHIN_DL = PHIN_LS - 0.03 SNP Log
CASE 3b: PHIN_DL = PHIN_LS - 0.03 CNL Log
CAUTION: IF final porosity < 0.05, ose more rigorous model shown
below.
 MORE RIGOROUS METHODS FOR
PHINm
MORE RIGOROUS METHODS FOR
PHINm
If the log is recorded in limestone units and a more accurate
lithology correction is desired, use the following formulae.
CAUTION: There are ,many tool variations with specific charts
for each. The equations below are two published versions and are
not guaranteed to be correct or appropriate for your case -
check the specific chart for your tool to be sure.
If lithology is quartz and tool type is SNP:
CASE 4a: PHIN_SS = 0.222 * PHIN_LS^2 + 1.021 * PHIN_LS + 0.024
Schlumberger SNP
CASE 4b: PHIN_SS = - 0.14 * PHIN_LS^2 + 1.047
* PHIN_LS + 0.0482 Dresser Atlas SNP
If lithology is dolomite and tool type is SNP:
CASE 5a: PHIN_DL = 0.60 * PHIN_LS^2 + 0.7490 * PHIN_LS - 0.00434
Schlumberger SNP
CASE 5b: PHIN_DL = 0.34 * PHIN_LS^2 + 0.8278 * PHIN_LS -
0.01249 Dresser Atlas SNP
If lithology is quartz and tool type is CNL:
CASE 6a: PHIN_SS = 0.222 * PHIN_LS^2 + 1.021 * PHIN_LS + 0.039
Schlumberger CNL
CASE 6b: PHIN_SS = PHIN_LS + 0.04
Dresser Atlas CNL
CASE 6c: PHIN_SS = - 0.4778 * PHIN_LS^2 + 1.220 * PHIN_LS
+ 0.0311 Welex/Halliburton CNL
If lithology is dolomite and tool type is CNL:
CASE 7a: PHIN_DL = 1.40 * PHIN_LS^2 + 0.389 * PHIN_LS - 0.01259 Schlumberger CNL
CASE 7b: IF PHIN_DL < 0.10 THEN PHIN_DL = 3.11 * PHIN_LS^2 +
0.102 * PHIN_LS - 0.00133 Dresser
Atlas CNL
ELSE PHIN_DL = PHIN_LS - 0.06
CASE 7c: PHIN_DL = 1.397 * PHIN_LS^2 + 0.345 * PHIN_LS - 0.0152
Welex/Halliburton CNL
If no lithology correction is needed.
CASE 8: PHINm = PHIN_LS
Finally:
PHINm = SELECT CASE
Where:
PHIN_LS = original neutron log reading in Limestone units
PHINm = apparent neutron log porosity corrected for lithology
(fractional)
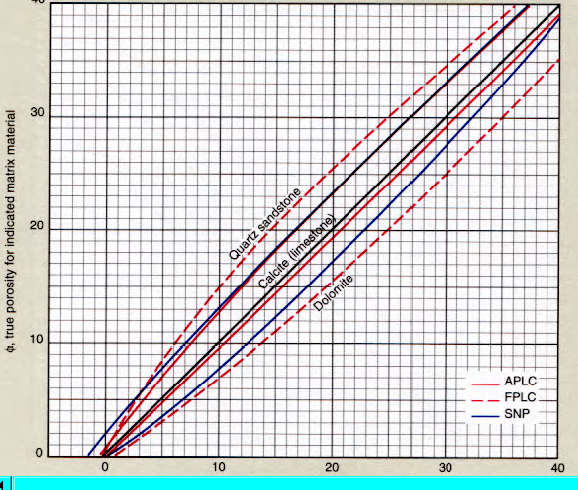
SNP neutron chart for lithology and scale
conversions, including salinity corrections (red lines)
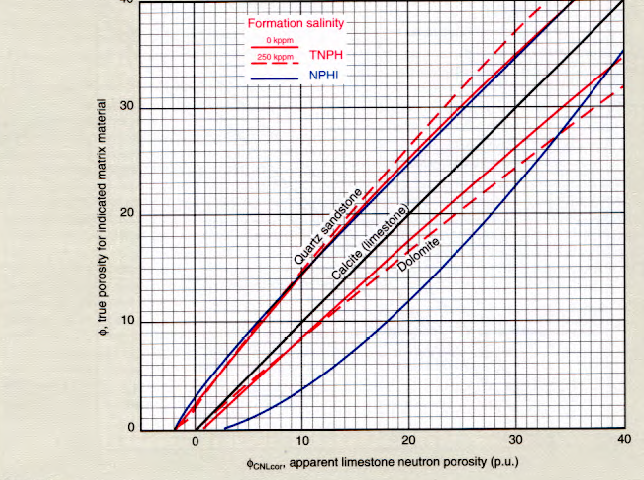
CNL neutron chart for lithology and scale conversions, including
salinity corrections (red lines)
The charts and math shown above are for older CNL and SNP type
neutron logs (NPHI curve). More modern CNL tools have additional
porosity transforms (eg TNPH). Refer to the appropriate service
company correction chart for newer tools. In particular,
epithermal CNL logs have considerably less lithology correction.
 NEUTRON LOG PARAMETERS
NEUTRON LOG PARAMETERS
|