Porosity from the Density Log
The density log is widely used to estimate porosity. The method works well when shale volume and matrix rock density are accurately known. Errors as large as 12% porosity can occur, and 3 to 6% are common if incorrect assumptions are made.

If both density and neutron logs are available, a superior model that does not require matrix rock properties is the Shale Corrected Density Neutron Complex Lithology Crossplot Method. The Meta/Kwik spreadsheet for this model is available at Downloads and Spreadsheets. 

Density Log RESPONSE EQUATION
The response equation for the density log in porosity units follows the classical form:
      1: PHID = PHIe * Sxo * PHIDw                                          (water term)
                  + PHIe * (1 - Sxo) * PHIDh                                    (hydrocarbon term)
                  + Vsh * PHIDsh                                                     (shale term)
                  + (1 - Vsh - PHIe) * Sum (Vi * PHIDi)                      (matrix term)

Where:
  PHIDh = log reading in 100% hydrocarbon
  PHIDi = log reading in 100% of the ith component of matrix rock
  PHID = log reading
  PHIDsh = log reading in 100% shale PHIDw = log reading in 100% water
  PHIe = effective porosity (fractional)
  Sxo = water saturation in invaded zone (fractional)
   Vi = volume of ith component of matrix rock
  Vsh = volume of shale (fractional)

To solve for porosity from the density log, we assume PHIDh, PHIDi, PHIDsh, PHIDw, and Vsh are known. We also assume PHIDw = PHIDh and Sxo = 1.0 when no gas is present. If gas is indicated, we make assumptions about PHIDh and Sxo, usually in the form of a correction factor to the gas free case, as described later.

This response equation is rigorous. Mineral and fluid parameters are shown HERE. Shale properties are selected from the log in an obvious shale zone.

References:
 

 1.  Logging Empty Holes
      C.G. Rodermund, R.P. Alger, J. Tittman, Oil and Gas Journal, 1961

 2. Formation Density Log Application in Liquid-Filled Holes
     R.P. Alger, L.L. Raymer, W.R. Hoyle , M.P. Tixier, JPT, 1964

 3.  Litho-Density Log Interpretation
      J.S. Gardner, J.L. Dumanoir, SPWLA, 1980

POROSITY FROM Density Log
Calculate density porosity from density data.
      2: PHID = (DENS - DENSMA) / (DENSW - DENSMA)

Apply density shale correction:
      3: PHIDSH = (DENSH - DENSMA) / (DENSW - DENSMA)
      4: PHIdc = PHID - Vsh * PHIDSH

Apply density gas correction.
      5: IF DENSITYGASSWITCH$ = "ON"
      6: THEN PHIdc = KD * PHIdc

Where:
  DENS = density log reading in zone of interest (gm/cc or kg/m3)
  DENSMA = density log reading in 100% matrix rock (gm/cc or kg/m3)
  DENSSH = density log reading in 100% shale (gm/cc or kg/m3)
  DENSW = density log reading in 100% water (gm/cc or kg/m3)
  KD = density log gas correction (fractional)
  PHID = porosity from uncorrected density log (fractional)
  PHIdc = porosity from density log corrected for shale (fractional)
  PHIDSH = apparent density log porosity of 100% shale (fractional)
  Vsh = shale volume (fractional)

COMMENTS:
A graphical solution, with shale correction, is shown below.

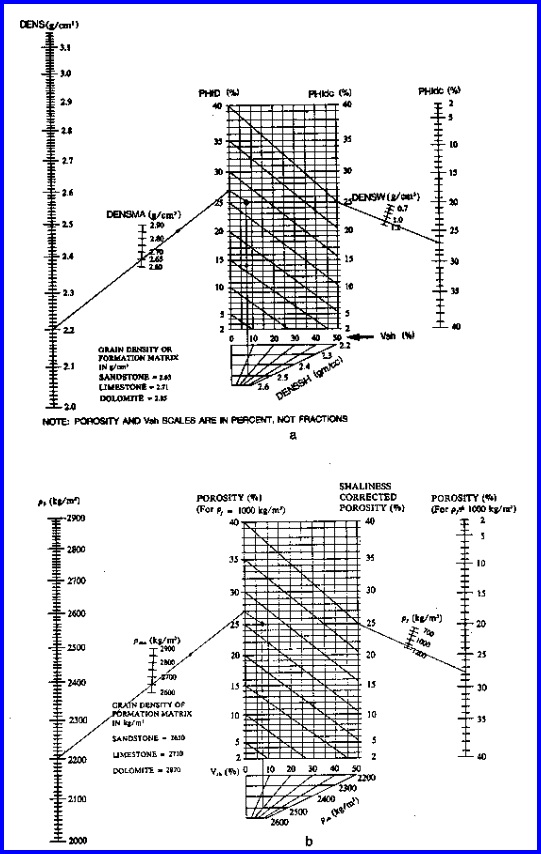
Chart for Estimating Shale Corrected Density Porosity

The density log corrected for shale is a very good approximation to porosity, but the log was not common before 1965, so sonic or neutron methods may be necessary for wells drilled before that time.

KD is in the range of 0.5 - 1.0 depending on invasion, gas density and local experience. A correction is almost always needed if gas is present.

Use gas correction only if PHIdc is too high compared to other sources and if gas is known to be present. This correction may be necessary even in shaly sands, since the depth of investigation of the density log is deep enough to see beyond the flushed zone.

WHEN DENSITY LOG IS IN POROSITY UNITS, POROSITY MAY BE WRONG BECAUSE THE POROSITY SCALE DOES NOT MATCH THE ROCK MINERALOGY. SEE NEXT SECTION FOR CORRECTIONS.

If density porosity data is in percent, rather than fractional, divide the data values by 100 before Step 2 and 3 are applied.

No compaction correction is made to density log data.

 

NUMERICAL EXAMPLE:
1. Assume a zone with:
    DENS = 2.15 gm/cc
    DENSW = 1.00 gm/cc
    DENSMA = 2.65 gm/cc
    Vsh = 0.33
    DENSSH = 2.60 gm/cc

    PHID = (2.15 - 2.65) / (1.00 - 2.65) = 0.30
    PHIDSH = (2.60 - 2.65) / (1.00 - 2.65) = 0.03
    PHIdc = 0.30 - 0.33 * 0.03 = 0.29
No gas correction is required.

Porosity From Density Log With Matrix Offset
One step that is often required is to convert apparent porosity on the density log into density units, then reconstitute porosity from this value corrected for a desired matrix and fluid value. This is done by rearranging the response equation of the previous section.

Calculate density from density porosity.
      7: DENS = (PHID * KD1 + (1 - PHID) * KD2

Where:
           English Units   Metric Units    Log Scale
  KD1       1.00                 1000               All
  KD2       2.65                 2650           Sandstone
  KD2       2.71                 2710           Limestone
  KD2       2.87                 2870           Dolomite

Calculate shale density.
      8: DENSSH = (PHIDSH * KD1 + (1 - PHIDSH) * KD2

Calculate porosity with new matrix and fluid.
      9: PHIDm = (DENS - DENSMA) / (DENSW - DENSMA)
      10: PHIDSHm = (DENSSH - DENSMA) / (DENSW - DENSMA)
      11: PHIdc = PHIDm - Vsh * PHIDSHm

Apply density gas correction.
      12: IF DENSITYGASSWITCH$ = "ON"
      13: THEN PHIdc = KD * PHIdc

Where:
  DENSSH = density log reading in 100% shale reconstituted from density porosity data (gm/cc or kg/m3)
  DENS = density value reconstituted from density porosity data (gm/cc or kg/m3)
  DENSMA = matrix density (gm/cc or kg/m3)
  DENSW = fluid density (gm/cc or kg/m3)
  PHID = porosity from uncorrected density log (fractional)
  PHIdc = porosity from density log corrected for shale (fractional)
  PHIDm = density porosity log reading corrected for matrix offset (fractional)
  PHIDSH = density porosity log reading in 100% shale (fractional)
  PHIDSHm = density porosity log reading in 100% shale corrected for matrix offset (fractional)
  Vsh = volume of shale (fractional)

COMMENTS:
See previous Section above.

ANCIENT DENSITY LOGS
Ancient density logs, and many modern slimhole density logs, are recorded in gamma ray counts per second. You get to work out the transform to density using a semi-logarithmic High - Low porosity technique as described for the neutron log. Here, high count rate = low density = high porosity. Semi-log crossplots of count rate versus core density or core porosity will calibrate the method. These tools have a single detector and are not compensated for borehole effects. Slim hole versions were widely used in strat holes and in mineral exploration projects. Charts for some specific tools can be found in the literature, such as the one shown below.

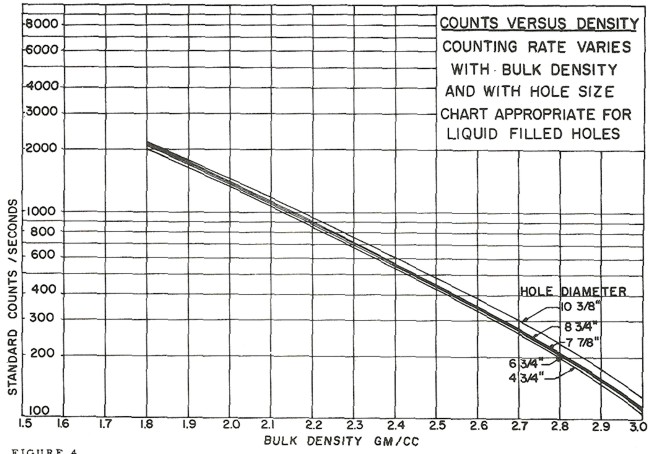
Counts per second to density transform for a Schlumberger PGT-A density tool. Each tool iteration and each service company requires a specific chart. Density varies with hole size  mud weight, and  , An equation for the 8 inch borehole case is DENScps = -0.88 * LOG(CPS) + 4.71

These tools are severely affected by hole size, mud weight, mud cake thickness, source type and strength, source detector spacing, and detector efficiency. The High-Low calibration method compensates for all these problems, but available charts do not. In the earliest versions of these tools, the source strength decayed  rapidly, so count rates definitely need to be normalized on a well by well basis.

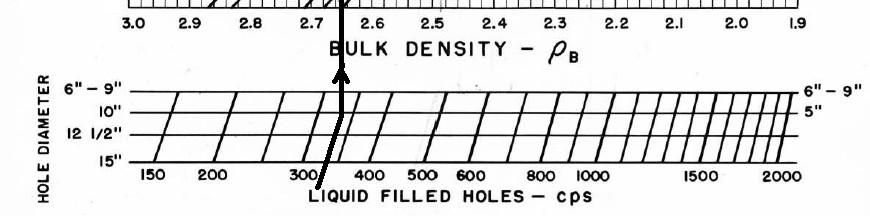
Most density transforms never made it into published chart books. This one did - Schlumberger PGT-C or D density count rates to porosity. Additional charts are available to correct for mud cake thickness and mud weight, and for air-filled holes. The count rate charts appeared in 1966 chart books, well after they were no longer needed, and disappeared after 1968. Most density count rate charts are very hard to find unless you have a good supply of ancient chart books from 1958 through 1968 - a 10 CD set of ancient chart books was published by Denver Well Log Society and sold through SPWLA.

DENSITY LOG PARAMETERS
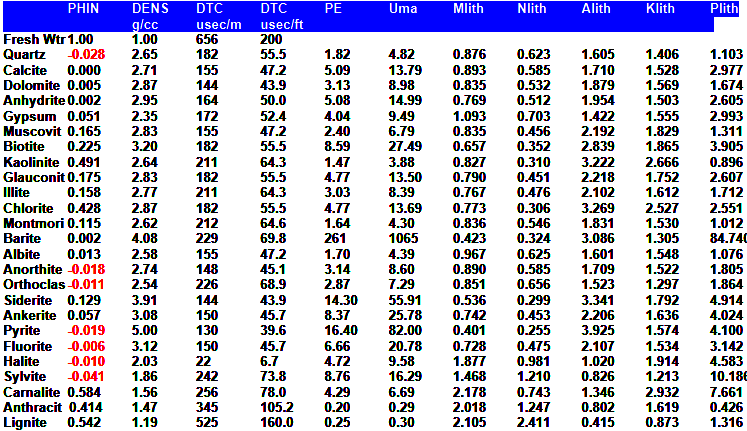
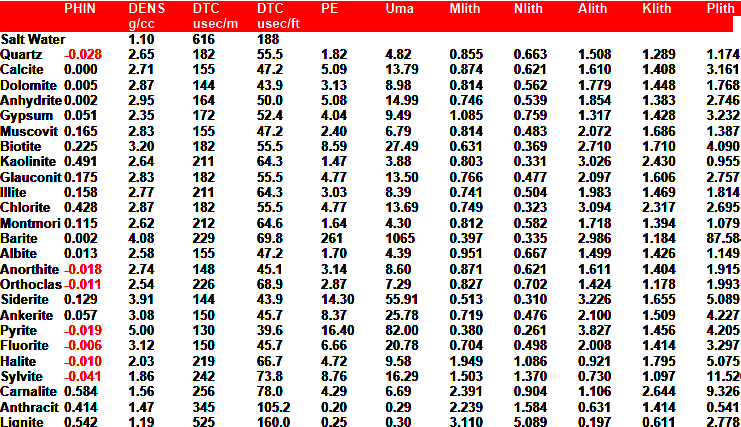