|
 INDUCTION LOG BASICS
INDUCTION LOG BASICS
This page describes induction logs
profiles, in the order of their appearance over the years.
This presentation style provides insights into tool
evolution, and a specific tool’s capabilities and
limitations. You will find most these tool types in your
well files – here’s your chance to learn more about them.
The induction log
was invented by Henry Doll of Schlumberger and described in 1947. It
was developed from electromagnetic research undertaken during World
War II on mine detectors. The first commercial success for the tool
began in 1956. Many evolutionary developments have occurred over the
last 50 years, providing better vertical resolution and deeper depth
of investigation.
Conventional
induction logs measure conductivity perpendicular to the axis of the
tool. In a vertical well, this is the horizontal direction. Vertical
conductivity may be quite different. Recent developments have
introduced a log that can measure vertically as well as
horizontally. It is in the commercialization phase of development,
and promises to be very useful in thin bedded and dipping reservoir
rocks.
The tool works in air, oil,
or mud filled open holes but salt muds give poor results, although
the array induction can handle saltier muds than earlier versions of
the tool. It does
not work in cased holes. A cased hole formation resistivity log is
available; it is a form of
laterlog.
Use the links in the right hand menu to skip the hairy technical
parts, although a little knowledge of electromagnetics, geometric
factors, and skin effect won't actually fry your brain.
References:
1. Introduction to
Induction Logging and Application to Logging of
Wells Drilled With Oil
Base Mud
H.G. Doll, AIME, 1949
2. Dual Induction-Laterolog: A New Tool for Resistivity Analysis
M.P. Tixier, R.P. Alger, W.P. Biggs, B.N. Carpenter, AIME,
1963
3. Introduction to the Phasor Dual Induction
Too
T.D.
Barber, JPT, Sept 1985
4. Using a Multiarray Induction Tool to Achieve Logs with Minimum
Environmental Effects
T.D.
Barber,, SPE paper 22725,,Oct 69, 1991
 INDUCTION LOG THEORY -- CRAIN'S HIGHLY SIMPLIFIED VERSION
INDUCTION LOG THEORY -- CRAIN'S HIGHLY SIMPLIFIED VERSION
Induction logs are designed to measure the conductivity of rock
formations by using the electromagnetic principles outlined by
Faraday, Ampere, Gauss, Coulomb and unified in a single theory
by James Maxwell in 1864.
The process involves the interaction of magnetic and electric fields:
1. alternating
current applied to transmitter coils
2. creates alternating magnetic field in rocks
3. which generates alternating current in rocks (current loops, eddy
currents)
4. current loops generate out of phase magnetic field in rocks
5. which generates in-phase voltage in receiver coils
6. calculate resistivity Rt = RES = K * V / I
The basic
equations for a single transmitter – receiver coil pair, in
EXTREMELY simplified form, are shown below.
1: Bt = uo * dI/dt
magnetic field due to current “I” in transmitter coil
2 : I
= C * dBt/dt current in formation induced by magnetic field “Bt”
3: Br = uo * dI/dt
magnetic field due to current “I”
circulating in the rock
4: V = N * A * (dBr/dt) voltage induced in receiver coil by
magnetic field Br
Where;
Bt = the magnetic field strength in the formation created by an
induction log transmitter
uo = the magnetic permittivity
dI/dt = rate of change of the current in the transmitter coil
I
= current circulating in the rock
C =
conductivity of rock
dBt/dt
= rate of change of transmitted magnetic field
Br = out-of-phase magnetic field strength in the formation created
by the currents in the rock
dI/dt = rate of change of the current in the rock
V = voltage induced in an induction log receiver coil
N = number of turns on the coil
A = area of the coil
dBr/dt
= rate of change of the magnetic field created by the currents
circulating in the rock
The magnetic fields,
and currents in the rock and receiver-transmitter system are
vectors (amplitude and direction). The in-phase component measured
at the receiver coil is called the Real (or R) component. The signal
that is 90 degrees out of phase is called the Imaginary (or X)
component. Older tools could measure only the R component. Newer
tools measure both R and X components. The X component is used to
enhance bed resolution by use of proprietary algorithms.
If
you can handle advanced calculus and know what the “curl” operator
does, refer to “Basic Theory of Induction Logging” by J.H. Moran
and K.S. Kunz, SEG Oct 1959 for the real story on induction log
theory.
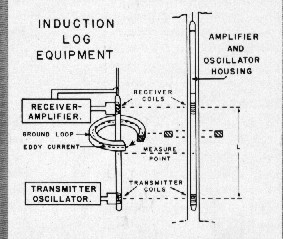 The
illustration at right shows a simple two coil induction log and a
single "ground loop" of current circulating in the rock around the
tool. An infinite number of ground loops exist, but only those near
the tool will generate a magnetic field strong enough to produce a
voltage in the receiver coil. The
illustration at right shows a simple two coil induction log and a
single "ground loop" of current circulating in the rock around the
tool. An infinite number of ground loops exist, but only those near
the tool will generate a magnetic field strong enough to produce a
voltage in the receiver coil.
Early induction logging tool consists of several
transmitter-receiver coil pairs within a logging tool housing. A
20,000 Hz regulated alternating current is produced in the
transmitter coils, which induces eddy currents by electromagnetic
induction into the rocks surrounding the coil system. The eddy
currents generate a magnetic field, which in turn induces voltages
in the receiver coils. By keeping the transmitter current constant,
the magnitude of the eddy currents are proportional to the
conductivity of the formation and 90 degrees out of phase with the
transmitter current. Voltages at the receiver coil induced by these
eddy currents are also proportional to the formation conductivity
and approximately in phase with the transmitter current. The
electronic circuitry of the receiver is designed to detect the
in-phase component of the receiver coil voltage and this serves as a
measure of the conductivity of the formation.
The eddy currents induced in a conductive formation
experience phase shift and attenuation. The loss due to attenuation
is known as skin effect (or propagation loss) and is corrected by
proprietary service company algorithms. Corrections fir the effect
of drilling fluid invasion may be required. Charts and computer code
are available for this purpose.
More modern induction tools use multiple frequencies and multiple coil spacings, along with measurements of both in-phase and quadrature
phase signal components. This allows numerical solutions for invaded
zone resistivity (Rxo) and true resistivity (Rt). These "answer"
curves are available to be presented along with the measured curves.
When Rt is provided, no further invasion corrections are required.
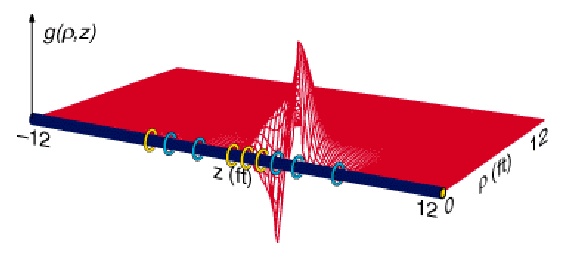
 RADIAL and VERTICAL GEOMETRIC FACTORS
RADIAL and VERTICAL GEOMETRIC FACTORS
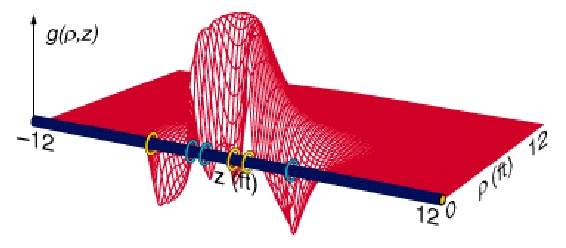
The voltage at the
receiver from a unit loop of radius, r, and altitude, z, with
respect to the center of the coil system is given by: Vr =
K * G * COND, where K is a function of the area of the transmitter
and receiver coils, distance between the coils, current in
the transmitter, and frequency of the transmitter current.
G is the geometric factor, which depends on the geometric position
of the unit loop as related to the transmitter and receiver
coils.
The radial geometric factor G considers
the formation as the combination of a large number of cylinders
coaxial with the borehole. The integrated radial geometric factor,
Gr, is the sum of all the G values for the total volume within
a cylinder of radius, r. This represents a thick homogeneous
formation invaded by mud filtrate where conductivity changes
radically, and includes a small portion of the borehole.
The signal measured by an Induction
log positioned opposite a thick formation usually reflects
the conductivity of that formation; however, in thin formations,
the signal is affected by the conductivities of the adjacent
formations. In a similar manner, the integrated vertical geometric
factor, Gv, becomes the sum of the G values for all of the
volume above (or below) a horizontal plane at a distance, z,
from the center of the coil span. The integrated vertical geometric
factor increases with the vertical distance, z, and must equal
unity for all space.
Development of the geometric factor
for a focused induction log can be accomplished by adding algebraically
all combinations of transmitter-receiver coil geometric factors
times each coil pair's contribution to the total instrument
response. This is done by computer modeling at the time the
tool is designed.
To illustrate the geometric factor
concept, assume borehole size = 8 in, invasion diameter = 40
in, Cm = 1000 mmho/m, Ci = 50 mmho/m, Cu = 100 mmho/m. For
a particular induction log, assume:
Gm = G8 = –0.001
Gi = G40 – G8 = 0.025 – (–0.001)
= 0.026
Gu = 1 - G40 = 1 – 0.025 = 0.975.
Where Cm, i, u = conductivity of the mud, invaded zone, and undisturbed zone
and Gm, i, u = radial geometric factor for the mud, invaded zone, and undisturbed
zone respectively.
1: CONDa
= Gm * Cm + Gi * Ci + Gu * Cu
= 1000
* (–0.001) + 50 * 0.026 + 100 *
0.975 = 97.8 mmho/m
The borehole and invasion create a
2.2 mmho/m error (100 – 97.8) in the measured value of
the un-invaded zone conductivity.
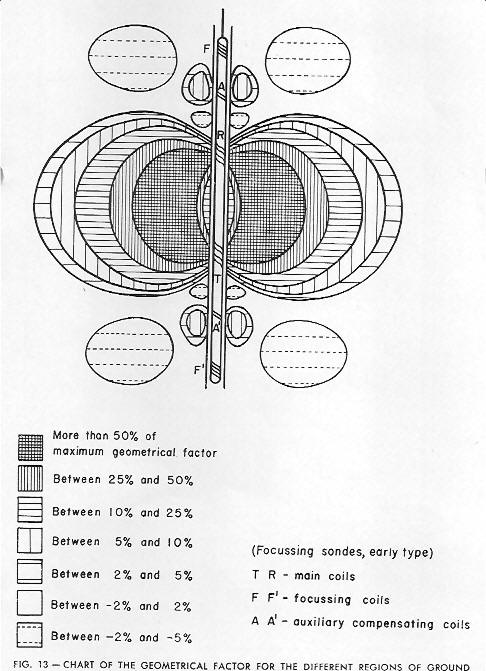
Illustration showing radial geometric factor for a 6
coil induction log
Bed thickness correction charts are
provided by service companies for their particular tools, based
on the vertical geometric factor concept. The following example
illustrates the geometric factor for thin bed response for
a typical logging tool:
Given:
Bed Thickness = 4 ft, CONDb = 100 mmho/m, CONDs = 1000 mmho/m,
Gb = 0.728,
Gs = 1 – 0.728 = 0.272,
where CONDb = conductivity of the bed of interest, and CONDs
= conductivity of the surrounding beds.
CONDa = 100 * 0.728 + 1000 * 0.272
= 345 mmho/m
The apparent conductivity is 3.45
times the actual conductivity of the zone (100 mmho/m), a 345%
error, illustrating the large error inherent in typical induction
log readings in thin beds. A resistive formation needs to be
at least 24 feet thick for the vertical geometric factor to
approach 1.0.
 BED BOUNDARIES ON INDUCTION LOGS
BED BOUNDARIES ON INDUCTION LOGS
Bed boundaries on induction logs
should be picked on the conductivity curve halfway between the high
and low conductivity values, as shown below.
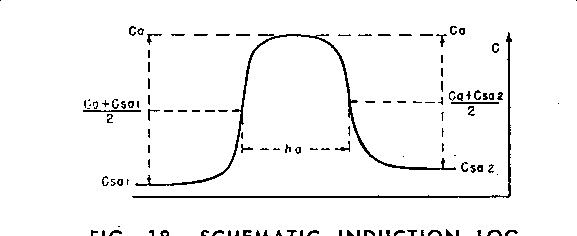
Depth of bed Boundary is chosen at mid-point of conductivity – not
the resistivity
Unfortunately, most modern induction logs display resistivity on a
logarithmic scale, not conductivity on a linear scale. As a result,
the mid-point rule is impossible to apply directly. You could do two
quick resistivity to conductivity conversions (COND = 1000 / RESD),
find the mid-point, and convert it back to resistivity (RESD = 1000
/ COND). This might be a bit onerous, so another rule is to pick the
resistivity inflection points, then move the top boundary of
resistive beds up 2 to 4 feet, and move the bottom down by
the same amount. Conductive beds get the same shift, but in the
opposite direction - make the bed thinner.
This
helps to compensate for the curve shape distortion caused by
transforming conductivity to resistivity. Newer induction logs have
better focusing and this stretch may not be needed - compare to core
or microlog or formation microscanner to see if a bed boundary shift
is needed. This shift is NOT required on Phasor or array induction logs.
The
illustration below shows the problem for a typical middle-aged
induction log (IES or DIL) These older logs were run for over 40
years so there are a lot of them in your well files.
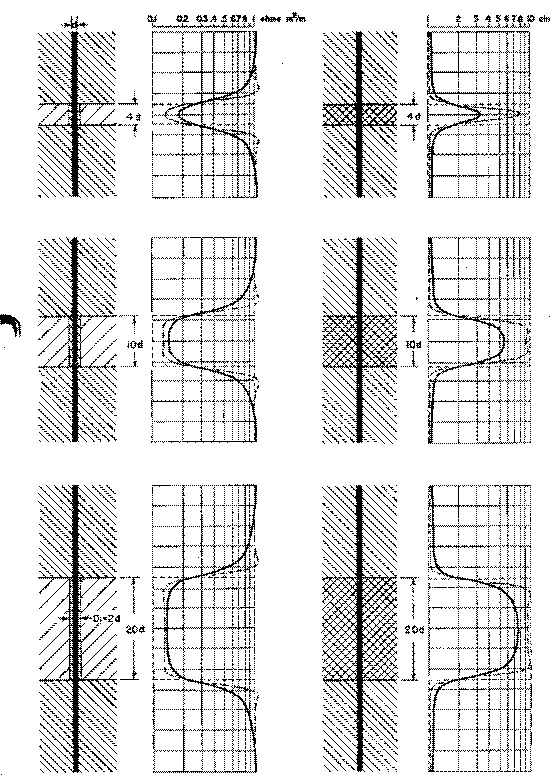
Bed boundaries on induction log
 INDUCTION ELECTRICAL SURVEY (IES) DETAILS
INDUCTION ELECTRICAL SURVEY (IES) DETAILS
This Section is based on a Schlumberger
document "Induction Response Theory
- the Basics". This may be part of "Induction Logging Manual", available
as a download from slb.com. Other service companies have provided
similar services to those described here. Images courtesy of
Schlumberger.
 The
induction electrical log (IES) is well defined by its name; it
consists of a deep investigation conductivity measurement combine
with a shallow resistivity and SP curves from the older electrical
survey. The presentation was made as close as possible to the ES,
with linear resistivity in Track 2 and linear conductivity in Track
3, replacing the lateral curve on the ES. The
induction electrical log (IES) is well defined by its name; it
consists of a deep investigation conductivity measurement combine
with a shallow resistivity and SP curves from the older electrical
survey. The presentation was made as close as possible to the ES,
with linear resistivity in Track 2 and linear conductivity in Track
3, replacing the lateral curve on the ES.
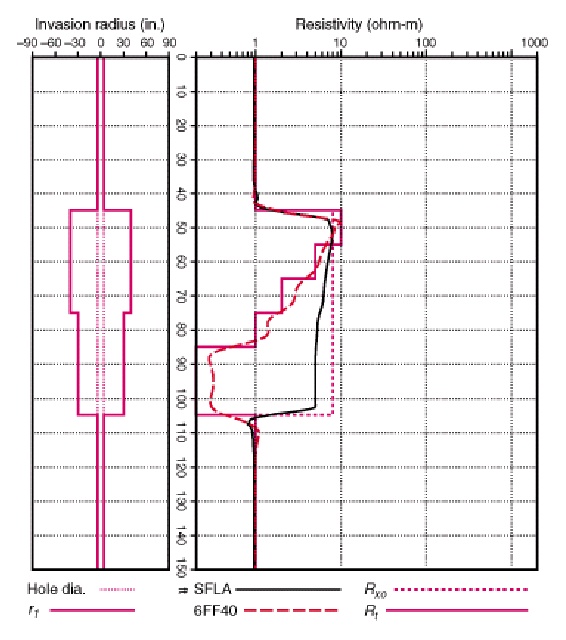
 THE 5FF27 and 5FF40 TOOLS
THE 5FF27 and 5FF40 TOOLS
There were 3 flavours of IES over the years -- the original; 5FF27
(1952), the 5FF40 (1955), and the 6FF40 (1959), which became the
industry standard for more than 30 years. In the tool designation,
the first digit represented the number of coils, "FF" stood for
"fixed focus", and the last two digits represent the main coil-pair
spacing. The vertical resolution and depth of investigation were
about double that number in inches.
<== Timeline of induction log evolution
Induction logs need to "see" deep enough beyond the wellbore to read
reasonably accurate values for formation conductivity with a
minimum contribution from the borehole and invaded zone. They also
have to be focused well enough to avoid shoulder bed effects. This
is accomplished by using multiple coils to focus the measurement and
subtract borehole effects.
The first commercial induction tool was the 5FF27 array, which was
introduced in the Gulf of Mexico and Gulf Coast in 1952. Although it
had low skin effect (necessary in that high-conductivity
environment), its depth of investigation was insufficient.
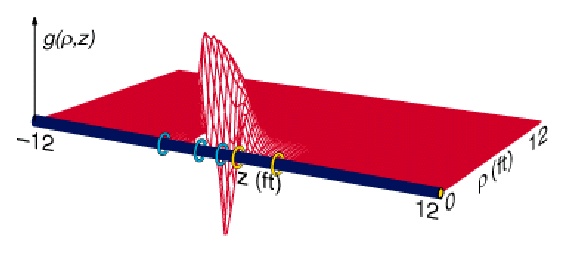
5FF27 response was unsymmetrical and negative coils caused
overshoot and spikes at bed boundaries and in rough hole.
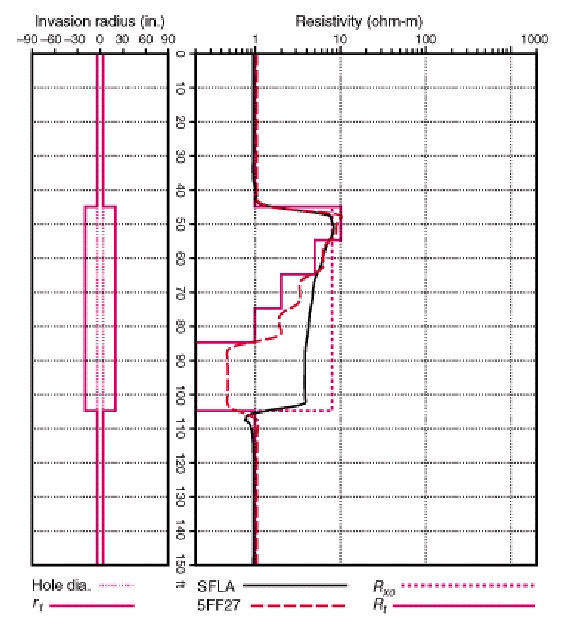
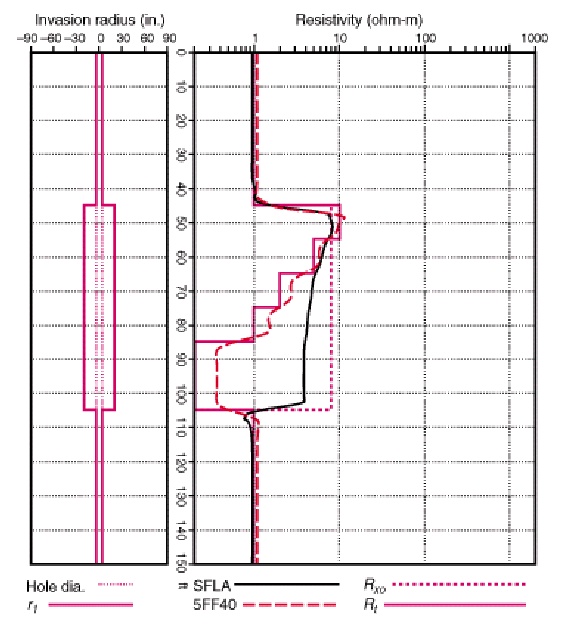
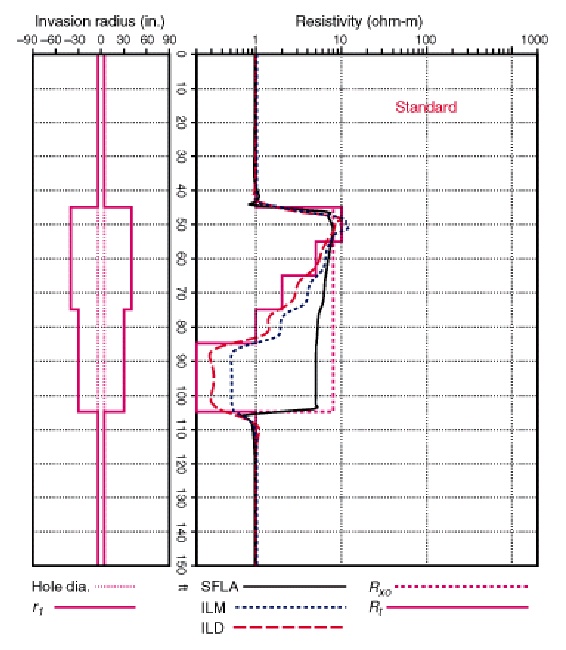
Calculated 5FF27 (left) and 5FF40 (right) responses for moderate
invasion compared to model. 5FF40 has better response un the higher
resistivity but bed boundaries are not as sharp. SFLA curve
represents a 16-jnch normal (shallow resistivity) curve which was
recorded on these logs, along with the SP curve.
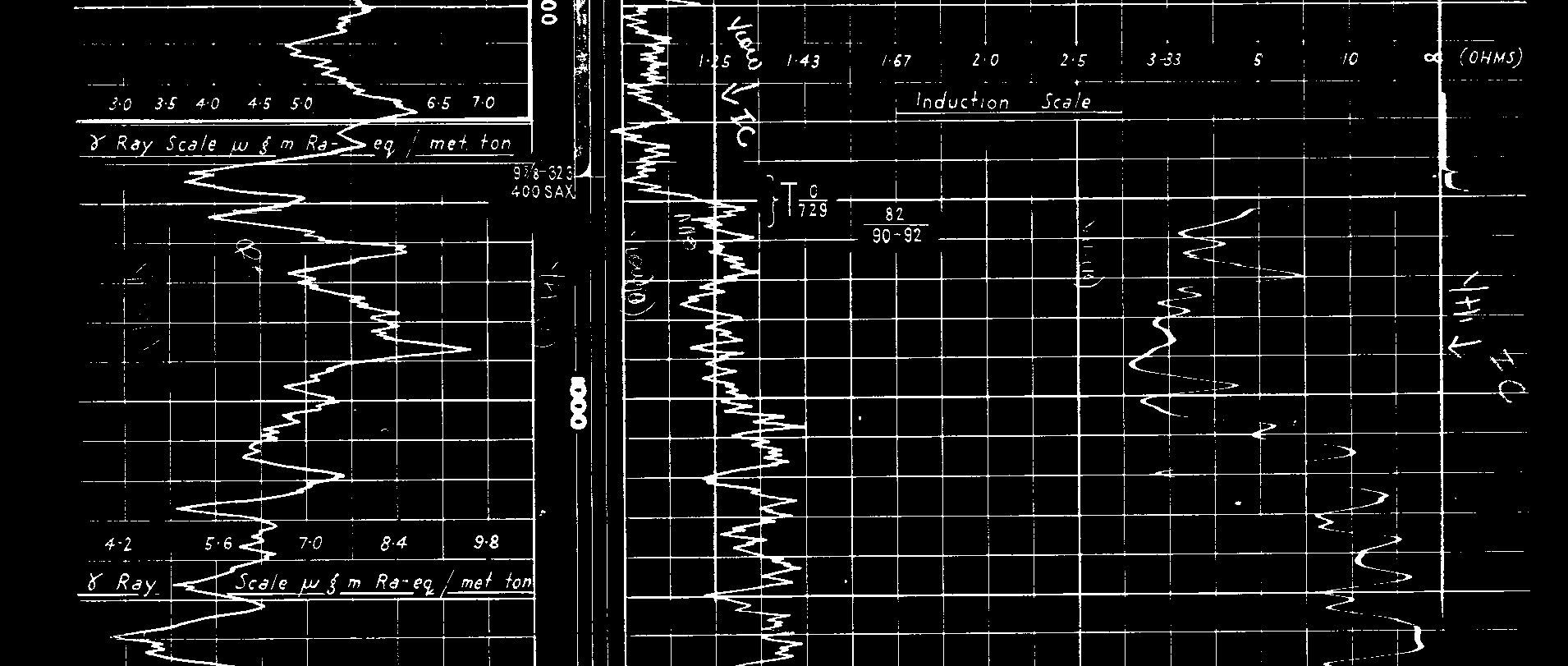
Heading and a portion of a very early induction conductivity log run
in 1954, with handwritten non-linear resistivity scale running from
1.0 ohm-m to infinity, derived from the conductivity curve
scale of 1000 to 0 mS/m (across the full width of the log).
The log appears to have been run simultaneously with the gamma ray
and neutron logs in Tracks 1 and 2.
  THE 6FF40 TOOL
THE 6FF40 TOOL
Schlumberger introduced what became the industry-standard induction
array, the 6FF40 array, in 1959. This array was licensed and
run, with minor variations, by almost all service companies. The
6FF40 array and its dual induction successor, the deep induction
array were the industry standard for 30 years. As was the case for
earlier tools, the signals from the coil sets were merged in analog
circuits in the tool body before being sent up hole.
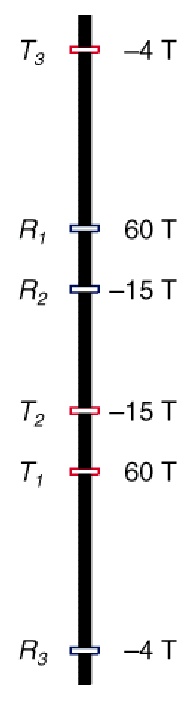
Coil arrangement on 6FF40 tool. Number and polarity of
coil windings shown on right side of image ==>
Response for 6FF40 tool is more symmetrical and sharper than for the
5FF40.
The effective length of the 6FF40 sonde is 61 inches, which is
significantly larger than the main-coil spacing of 40 inches. This
helps to explain why the sonde is unable to resolve beds thinner
than 5 feet and also why it reads much deeper than a 40-inche
two-coil sonde.
To add to the confusion,
the
standard resolution 6FF40 ILD logs has a resolution width of 8 feet.
Comparison of 5FF40 (left) and 6FF40 (right) in the simulated rock
sequence. Depth of invasion (shown in Track 1) is much deeper on the
6FF40 model.
Because of the invasion, the logs are only qualitative as to Rt,
especially in the low resistivity zones.
 DUAL
INDUCTION LOG (DIL) DETAILS
DUAL
INDUCTION LOG (DIL) DETAILS
This Section is based on a Schlumberger
document "Induction Response Theory
- the Basics". This may be part of "Induction Logging Manual", available
as a download from slb.com. Other service companies have provided
similar services to those described here. Images courtesy of
Schlumberger.
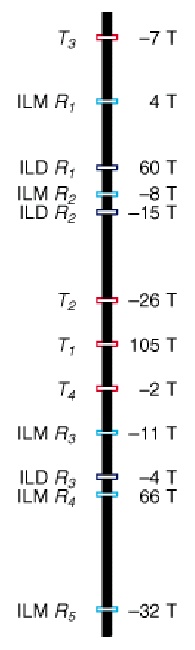 Dual
induction measurement was introduced in 1962 in an attempt to
quantify the effect of the invaded zone. The dual induction tool
kept the 6FF40 array as the deep measurement. The added shallower
induction measurement (medium induction) used the ILD
transmitter coils in combination with its own new receiver
configuration. This tool was referred to as the DIT-A.
Most of the ILM signal comes from within a radius of 60 inches,
whereas the ILD signal penetrates more than 100 inches. This was the
first log to provide linear and/or logarithmic resistivity scales on
the final log presentation. Dual
induction measurement was introduced in 1962 in an attempt to
quantify the effect of the invaded zone. The dual induction tool
kept the 6FF40 array as the deep measurement. The added shallower
induction measurement (medium induction) used the ILD
transmitter coils in combination with its own new receiver
configuration. This tool was referred to as the DIT-A.
Most of the ILM signal comes from within a radius of 60 inches,
whereas the ILD signal penetrates more than 100 inches. This was the
first log to provide linear and/or logarithmic resistivity scales on
the final log presentation.
In 1968, with the introduction of the second-generation DIT-B, an
additional small transmitter coil was added to both arrays to
improve the borehole response of the ILM. However, this coil does
not significantly affect the deeper ILD response, which remains
identical to 6FF40 log for all practical purposes.
Dual induction deep and medium coil arrays ==:
A shallow measurement provided by a laterolog tool is also included
when the dual induction tool is run. The LL8 tool was used on early
dual induction tools. It was replaced in the mid-1970s by the SFL
Spherically Focused Resistivity log, a laterolog tool with
considerably reduced borehole response.
The standard resolution ILD and ILM logs have resolution widths of 8
and 5 ft, respectively
ILM response. See previous Section for ILD (6FF40) response.
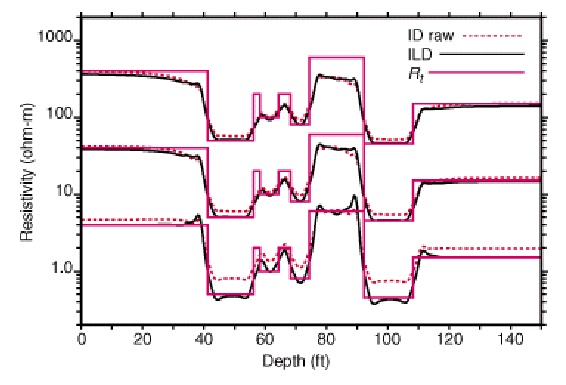
Comparison of 6FF40 (left) and DIL (right) in the simulated rock
sequence. Depth of invasion (shown in Track 1) is moderately
deep for both logs.
 Because
the 6FF40 and ILD arrays survey a relatively large volume of the
formation, response to beds of interest can be affected by adjacent
beds, invasion of the drilling mud or even the presence of the
borehole itself. In addition, skin effect causes a significant
nonlinear decrease in signal, especially in conductive formations.
Over the years, a series of correction algorithms has been derived
to compensate for these parasitic effects. The traditional method
for using these algorithms is to apply them individually in an
empirically defined sequence. This methodology is not correct in
principle because of the interaction of the induction fields with
all the media they penetrate. However, it provided a reasonably
accurate stopgap means of obtaining an accurate estimation of Rt for
many years. Because
the 6FF40 and ILD arrays survey a relatively large volume of the
formation, response to beds of interest can be affected by adjacent
beds, invasion of the drilling mud or even the presence of the
borehole itself. In addition, skin effect causes a significant
nonlinear decrease in signal, especially in conductive formations.
Over the years, a series of correction algorithms has been derived
to compensate for these parasitic effects. The traditional method
for using these algorithms is to apply them individually in an
empirically defined sequence. This methodology is not correct in
principle because of the interaction of the induction fields with
all the media they penetrate. However, it provided a reasonably
accurate stopgap means of obtaining an accurate estimation of Rt for
many years.
Example of conductivity boosting in three resistivity regimes. The
effect is only noticeable in low resistivity rocks ==>
For single and dual induction logs, charts were used to boost
conductivity and correct for invasion. Today this can be replaced by
stand-alone software. For Phasor and array induction tools, the work
is done in real-time as the logs are run and no further corrections
are needed.
 PHASOR
INDUCTION LOG (IDPH) DETAILS
PHASOR
INDUCTION LOG (IDPH) DETAILS
This Section is based on a Schlumberger
document "Induction Response Theory
- the Basics". This may be part of "Induction Logging Manual", available
as a download from slb.com. Other service companies have provided
similar services to those described here. Images courtesy of
Schlumberger.
The Phasor induction tool is basically the same as a dual induction
with deep, medium, and SFL measurements. Coil arrays, windings, and
response maps for deep and medium measurements are unchanged. The
major difference is the real-time processing to enhance resolution.
Rxo and Rt are derived so no additional environmental
corrections are needed.
Starting in the mid-1980s, new developments in electronics
technology, new work on computing the response of the induction tool
in realistic formation models, and modern signal processing theory
were combined to overcome these limitations in the Phasor Induction-SFL
tool. Central to the development of the Phasor tool was a nonlinear
deconvolution technique that corrects the induction log in real time
for shoulder effect and improves the thin-bed resolution over the
full range of formation conductivities. This algorithm, called "Phasor
Processing" uses the induction quadrature signal, or X-signal, which
measures the nonlinearity directly. Phasor Processing corrects for
shoulder effect and provides thin-bed resolution down to 2 ft in
many cases.
To sharpen bed boundaries and reduce shoulder bed effects, an inverse filter
is used.
The filter is a set of weights, each of which is multiplied by the
corresponding log reading and then summed to produce a single depth
sample of the corrected log. Because the ILD measurement includes
information from formation layers within 50 ft, the filter includes
measurement data from 50 ft on either side of the current depth. The
resulting filter covers 100 ft of log to produce a single depth
sample. The result of the inverse filtering process is a log that
more closely resembles the formation conductivity profile.
A
transformation from the X-signal to match the skin effect signal
exactly was also developed, which when added to the inverse-filtered
R-signal, forms a linear log that does not change its
character at high formation conductivities.
The standard- resolution IDPH and IMPH logs have resolution widths
of 8 and 5 ft, respectively, which are identical to the ILD and ILM
logs in resolution. The 3-ft resolution IDER and IMER logs are
matched in resolution. The 2-ft resolution logs are the IDVR and
IMVR logs. Not all wells can support high-resolution logs, due to
large borehole diameter.
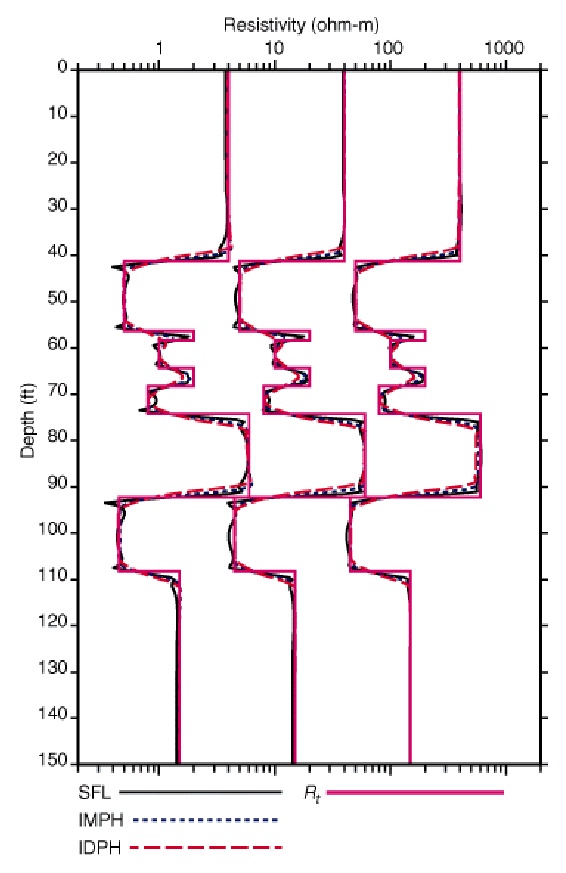 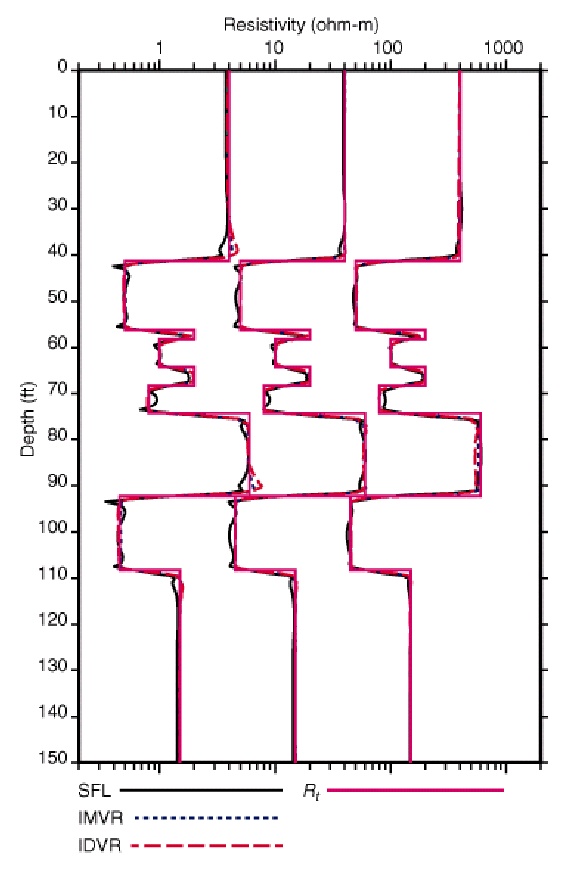
Standard resolution Phasor induction (left), 2-foot resolution (right)
 ARRAY
INDUCTION LOG (AIT) DETAILS
ARRAY
INDUCTION LOG (AIT) DETAILS
This Section is based on a Schlumberger
document "Induction Response Theory
- the Basics". This may be part of "Induction Logging Manual", available
as a download from slb.com. Other service companies have provided
similar services to those described here. Images courtesy of
Schlumberger.
 The
Phasor induction suffered in large boreholes and deep or complicated
invasion profiles. and was phased out in the mid to late 1990's. The
good ol' dual induction had been pushed to its technological limits
and could go no farther. The replacement was a totally new design --
the array induction tool (AIT). The log displays 5 resistivity
curves at depths of investigation ranging from 10 to 90 (or 120)
inches. Rxo and Rt are derived so no additional environmental corrections are
needed. Bed resolution can be computed to 1, 2, or 4 feet.
Resistivity and saturation images of the formation can be produced. The
Phasor induction suffered in large boreholes and deep or complicated
invasion profiles. and was phased out in the mid to late 1990's. The
good ol' dual induction had been pushed to its technological limits
and could go no farther. The replacement was a totally new design --
the array induction tool (AIT). The log displays 5 resistivity
curves at depths of investigation ranging from 10 to 90 (or 120)
inches. Rxo and Rt are derived so no additional environmental corrections are
needed. Bed resolution can be computed to 1, 2, or 4 feet.
Resistivity and saturation images of the formation can be produced.
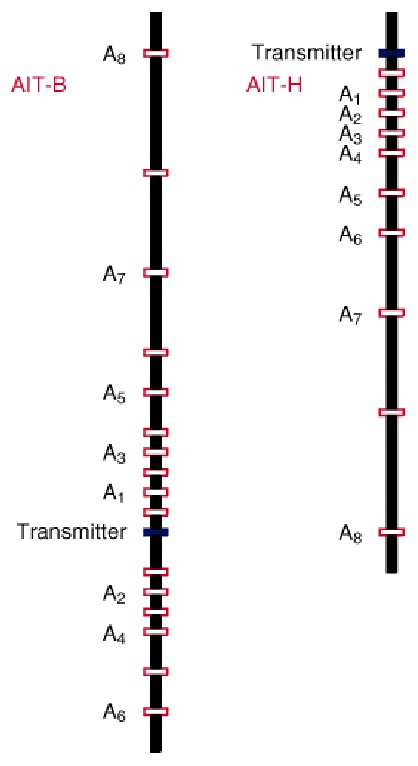
These tools abandon the concept of fixed-focus sensors and are
constructed of eight independent arrays with main coil spacings
ranging from 6 in. to 6 ft. Two AIT tools are presently in the
field: the AIT-B (standard AIT tool) and the shorter AIT-H (PLATFORM
EXPRESS AIT tool).
The AIT-B tool operates simultaneously at three frequencies;
in-phase and quadrature signals are acquired from every array at the
one or two frequencies suitable for that array length. The AIT-H
tool operates at a single frequency and measures the R- and
X-signals for each array. All these measurements, each with its
unique spatial response, are simultaneously acquired every 3 inches
of depth.
Exceptional stability is maintained over full temperature and
pressure ranges through the use of a patented metal mandrel and
ceramic coil forms; there are no fiberglass supporting structures in
the tool.
Each array consists of a single transmitter coil and two receivers.
In the AIT-H tool, some of the coils are co-wound.
Nonlinear processing methods have been developed that use each of
the measurements, combining them in such a way as to focus the log
response at a desired region in the formation that does not change
as formation conductivity changes. Several output logs can be
presented, each focused to a different distance into the formation.
Each of the new logs is a combination of several array measurements,
and all are interpretable as induction logs with full environmental
corrections. The logs are virtually free of cave effect and can
be used to provide Rt estimates with no built-in assumptions about
the invasion profile.
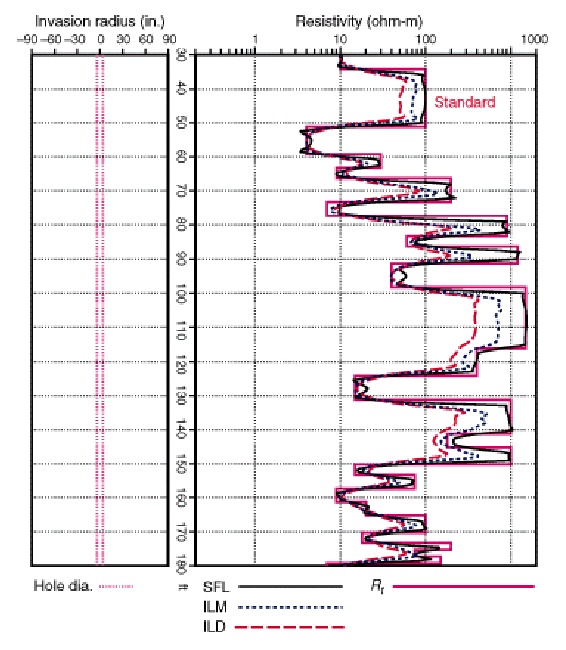 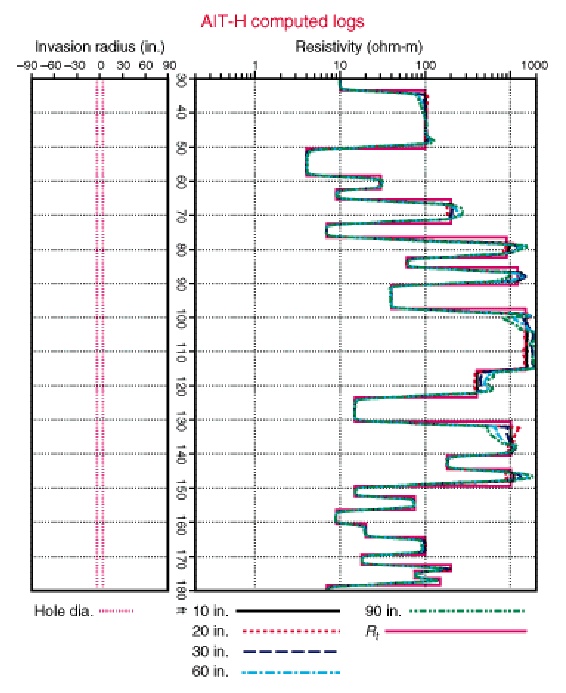
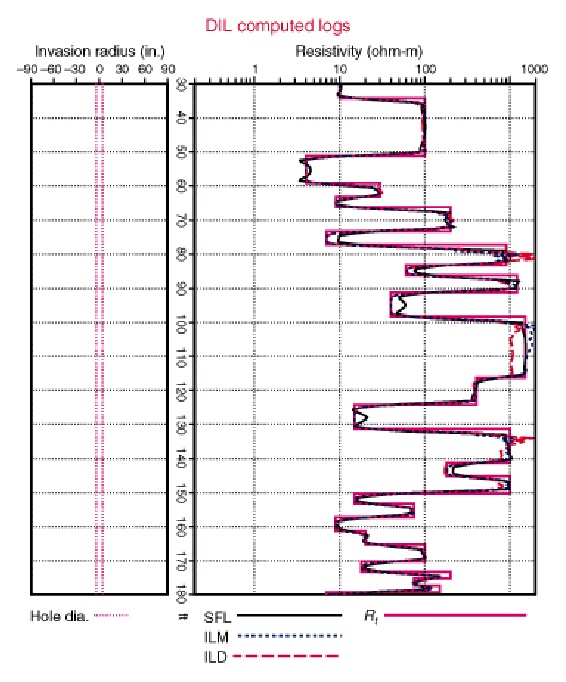
Computed DIL (left and AIT (right) shows effect of AIT's automatic
shoulder bed correction on high resistivity layers. AIT is 1-foot
resolution.
Computed Phasor induction 2-ft resolution (left and AIT 1-foot
resolution (right) shows AIT has better low resistivity results due
to automatic skin effect correction.
 INDUCTION LOG CURVE NAMES
INDUCTION LOG CURVE NAMES
Notes: * = optional curve. Abbreviations varied
between service companies - common abbreviations are shown as well
as the generic abbreviation as used elsewhere in this Handbook.
 Induction-Electrical
Survey (IES)
Induction-Electrical
Survey (IES)
|
Curves |
Units |
Abbreviations |
| 16"
normal |
ohm-m |
R16,
SN,
or RESS |
| induction
conductivity |
mS/m |
COND |
| induction
resistivity |
ohm-m |
RIL
or RESD |
| spontaneous
potential |
mv |
SP |
| *
gamma ray |
API |
GR |
 Dual
Induction - LL8 or SFL (DIL or ISF)
Dual
Induction - LL8 or SFL (DIL or ISF)
|
Curves |
Units |
Abbreviations |
| deep
induction resistivity |
ohm-m |
ILD
or RESD |
| medium
induction resistivity |
ohm-m |
ILM
or RESM |
| shallow
resistivity |
ohm-m |
RLL8
or RSFL or RESS |
| spontaneous
potential |
mv |
SP |
| *
gamma ray |
API |
GR
|
| *
quick look ratio |
frac |
Rxo/Rt |
| *
apparent water resistivity |
ohm-m |
Rwa |
| *
formation factor ratio |
frac |
Fr/Fs |
| * sonic travel time |
usec/ft |
DELT or DTC |
| * density |
gm/cc |
RHOB or DENS |
 Phasor Induction Log (DIT-E)
Phasor Induction Log (DIT-E)
|
Curves |
Units |
Abbreviations |
| deep
phasor resistivity |
ohm-m |
IDPH
or RESD |
| medium
phasor resistivity |
ohm-m |
IMPH
or RESM |
shallow
resistivity
*
deep enhanced phasor resistivity |
ohm-m
ohm-m
|
RSFL
or RESS
IDER
or RESD |
| *
medium enhanced phasor resistivity |
ohm-m |
IMER
or RESM |
| *
deep very enhanced phasor |
ohm-m |
IDVR
or RESD |
| *
medium very enhanced phasor |
ohm-m |
IMVR
or RESM |
* Rxo
* Rt |
ohm-m
ohm-m |
RXO or RESS
RT or RESD |
| spontaneous
potential |
mv |
SP |
| *
gamma ray |
API |
GR |
| *
quick look ratio |
frac |
Rxo/Rt |
| *
apparent water resistivity |
ohm-m |
Rwa |
| *
formation factor ratio |
frac |
Fr/Fs |
 Array
Induction Log (AIT)
Array
Induction Log (AIT)
|
Curves |
Units |
Abbreviations |
| four
foot resistivity 10 inch depth |
ohm-m |
AF10,
AHF10, ASF10 (RESS) |
| four
foot resistivity 20 inch depth |
ohm-m |
AF20, AHF20, ASF20 |
| four
foot resistivity 30 inch depth |
ohm-m |
AF30,
AHF30, ASF30 (RESM) |
| four
foot resistivity 60 inch depth |
ohm-m |
AF60,
AHF60, ASF60 |
four
foot resistivity 90 inch depth
(see Special Features listed below) |
ohm-m
|
AF90,
AHF90, ASF90 (RESD) |
* Rxo
* Rt |
ohm-m
ohm-m |
RXO or RESS
RT or RESD |
| *
resistivity image |
Rwa,
or Sw |
image,
colour |
| *
spontaneous potential |
mv |
SP |
| *
mud resistivity |
ohm-m |
AHMF |
| *
gamma ray |
API |
GR |
| |
|
Note
1: Baker Atlas tool has 120 inch depth as well as
the 5 others, all with different mneumonics than Schlumberger. |
| |
|
|
|
Note
2: One foot and two foot curves may also be recorded
and displayed separately (AOxxx and ATxxx) as well as
environmentally corrected four foot resistivity (AExxx).
Some conductivity curves are also recorded but seldom
displayed. Extrapolated values for Rxo and Rt are also
generated for each of the 3 bed thickness resolutions. |
 EXAMPLES OF INDUCTION LOGS
EXAMPLES OF INDUCTION LOGS
Sample log presentations are shown below. The shallow resistivity curve has evolved over time, from
the 16” normal in the 1960’s, laterolog-8 (LL8) in the 1970’s,
spherically focused log (SFL) in the 1980’s, to a shallow (10”)
induction curve on the current array induction log.

Induction log showing logarithmic scale (left)
and linear scale (upper left) with conductivity curve as well
as resistivity curves. Many varieties of Induction logs are
run today, some with interpretive images of resistivity profiles
or saturation. Combination log presentations with porosity
curves, such as sonic (right) or density are found in some
locations. The SP and/or gamma ray curve is in track one.
Logarithmic scales compress the resistivity range into a smaller
space, reducing the need for backup scales.

Typical layout of a dual induction log or equivalent, with GR
and SP in Track 1, and shallow, medium, and deep resistivity on
logarithmic scale in the wide track. Note bad deep induction log and
low resistivity spikes caused by fractures. There is a 6 meter
transition zone into the water zone at the bottom of the log.
The newest array induction logs use multi-coils combined with
higher transmitter currents, plus very intensive inverse
modeling to obtain conductivity focused to 1, 2, or 4 feet.
Commercial software is available to perform similar inverse
modeling on older logs, but the results will not be equal to a
modern array induction because the software has much less data to
work from. It is still worth doing, but don't expect miracles.
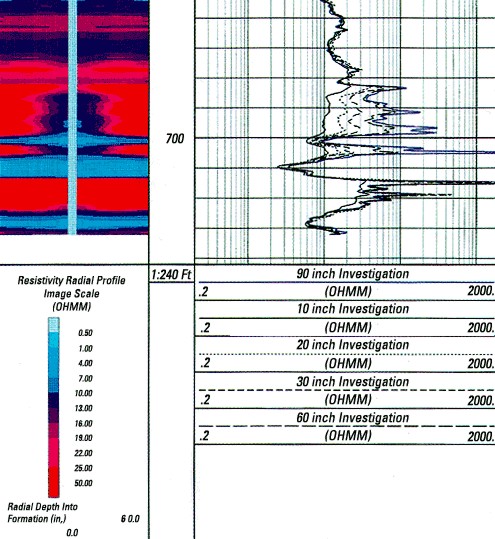
The standard presentation of an array induction log has 5 resistivity curves, with progressive depths of
investigation of 10, 20, 30, 60, and 90 inches. Some tools are
focused to reach 120 inches. A calculated value for Rxo and Rt are
often found in the digital data file. These are derived from the
inverse modeling of the inferred invasion profile using proprietary
algorithms. The invasion profile can be displayed as an image log.
|






 The
induction electrical log (IES) is well defined by its name; it
consists of a deep investigation conductivity measurement combine
with a shallow resistivity and SP curves from the older electrical
survey. The presentation was made as close as possible to the ES,
with linear resistivity in Track 2 and linear conductivity in Track
3, replacing the lateral curve on the ES.
The
induction electrical log (IES) is well defined by its name; it
consists of a deep investigation conductivity measurement combine
with a shallow resistivity and SP curves from the older electrical
survey. The presentation was made as close as possible to the ES,
with linear resistivity in Track 2 and linear conductivity in Track
3, replacing the lateral curve on the ES.







 Dual
induction measurement was introduced in 1962 in an attempt to
quantify the effect of the invaded zone. The dual induction tool
kept the 6FF40 array as the deep measurement. The added shallower
induction measurement (medium induction) used the ILD
transmitter coils in combination with its own new receiver
configuration. This tool was referred to as the DIT-A.
Dual
induction measurement was introduced in 1962 in an attempt to
quantify the effect of the invaded zone. The dual induction tool
kept the 6FF40 array as the deep measurement. The added shallower
induction measurement (medium induction) used the ILD
transmitter coils in combination with its own new receiver
configuration. This tool was referred to as the DIT-A. 

 Because
the 6FF40 and ILD arrays survey a relatively large volume of the
formation, response to beds of interest can be affected by adjacent
beds, invasion of the drilling mud or even the presence of the
borehole itself. In addition, skin effect causes a significant
nonlinear decrease in signal, especially in conductive formations.
Over the years, a series of correction algorithms has been derived
to compensate for these parasitic effects. The traditional method
for using these algorithms is to apply them individually in an
empirically defined sequence. This methodology is not correct in
principle because of the interaction of the induction fields with
all the media they penetrate. However, it provided a reasonably
accurate stopgap means of obtaining an accurate estimation of Rt for
many years.
Because
the 6FF40 and ILD arrays survey a relatively large volume of the
formation, response to beds of interest can be affected by adjacent
beds, invasion of the drilling mud or even the presence of the
borehole itself. In addition, skin effect causes a significant
nonlinear decrease in signal, especially in conductive formations.
Over the years, a series of correction algorithms has been derived
to compensate for these parasitic effects. The traditional method
for using these algorithms is to apply them individually in an
empirically defined sequence. This methodology is not correct in
principle because of the interaction of the induction fields with
all the media they penetrate. However, it provided a reasonably
accurate stopgap means of obtaining an accurate estimation of Rt for
many years.

 The
Phasor induction suffered in large boreholes and deep or complicated
invasion profiles. and was phased out in the mid to late 1990's. The
good ol' dual induction had been pushed to its technological limits
and could go no farther. The replacement was a totally new design --
the array induction tool (AIT). The log displays 5 resistivity
curves at depths of investigation ranging from 10 to 90 (or 120)
inches. Rxo and Rt are derived so no additional environmental corrections are
needed. Bed resolution can be computed to 1, 2, or 4 feet.
The
Phasor induction suffered in large boreholes and deep or complicated
invasion profiles. and was phased out in the mid to late 1990's. The
good ol' dual induction had been pushed to its technological limits
and could go no farther. The replacement was a totally new design --
the array induction tool (AIT). The log displays 5 resistivity
curves at depths of investigation ranging from 10 to 90 (or 120)
inches. Rxo and Rt are derived so no additional environmental corrections are
needed. Bed resolution can be computed to 1, 2, or 4 feet. 




