|
 Determining Dip By Clustering and Pooling
Determining Dip By Clustering and Pooling
This Section covers the dip calculation method that was
widely used for more than 25 years prior to the introduction
of the 4 pad, 8 button stratigraphic dipmeter. Pooling and
clustering results will be found in many thousands of well
files, so if you intend to use such dipmeters, it would pay
to know how the results were obtained.
The early approach for automatic determination of dip from a four
arm dipmeter was quite arbitrary. The selection
procedure was based on:
1. a distribution of closure errors
2. the elimination of the correlation curve associated with the
worst (lowest) correlation coefficient, resulting in a three arm
dip determination or, if no curve fitted this description, a compromise
(average) among the four possible solutions resulting from the
planarity error.
None
of these approaches used any geological knowledge or any sophisticated
statistical aids in the solution.
The
cluster approach for dip selection was developed by Schlumberger
to help eliminate the problem of closure and planarity errors.
The CLUSTER program name is a registered trademark of Schlumberger.
The CLUSTER program does no curve correlation; it operates on
output data from an existing dipmeter program. The best reference
is “Cluster - A Method for Selecting Most Probable Dip Results”,
V. Hepp and A. Dumestre, SPE Paper 5543, 19726.
The
CLUSTER method assumes that correlations are valid if they repeat
when the correlation window is moved over a small step distance.
If a dominant anomaly exists, it controls the correlation on at
least two adjacent dip computations, and it follows that the dominant
anomaly defines the same dip value for as long as it is included
inside the correlation window.
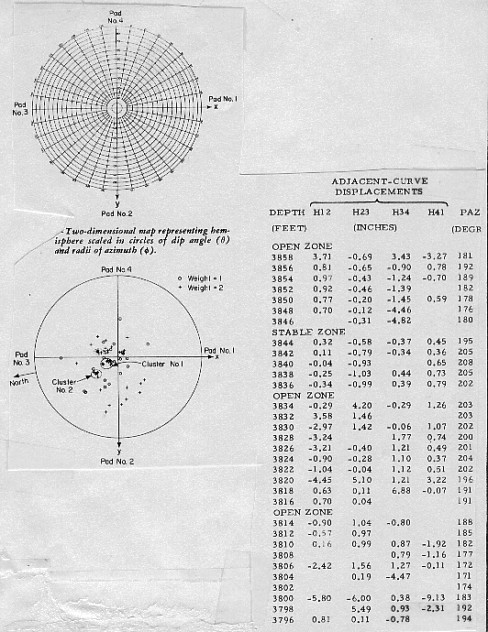
The
scattergram of points shown on the illustration below presents a
plot of all the dips computed from all the retained displacement
pairs of ten computation levels. Each dip is plotted at a location
on the plot defined by its magnitude and azimuth, and coded to
represent a weight indicating the quality of the correlation.
There is a great deal of scatter, indicating the noisy nature
of the correlated curves. However, two concentrations of points
of greater consistency, marked Cluster 1 and Cluster 2, are present.
Redundant
dip results thus allow us to choose groups of dips which show
some stability throughout the zone and to choose the displacement
combinations which contribute dips to the group. Since Cluster
1 represents the greatest concentration of dips, it should be
nearest to the dip defined by the dominant anomaly.
If
no displacement pair contributes to Cluster 1, then perhaps a
contribution is made to Cluster 2 and this, also, should be a
valid dip, even though the indication of consistency is not as
strong. Failing this, the displacement information must be regarded
as meaningless. For such levels no results will be printed on
the CLUSTER output listing.
In
the example below, ten levels were grouped together
from an arbitrarily selected interval. In the actual clustering
procedure an attempt is made to group levels together in a meaningful
fashion into short intervals or zones. Zoning is achieved by testing
the stability of successive adjacent curve displacements in the
input listing.
Detailed output from clustering of dip data
The
test for stability checks the displacement value in the next level
upwards to see if it is similar to the current one. If this test
is satisfied, over several consecutive levels in at least two
contiguous adjacent curve displacement columns, the zone is stable.
Zones that do not satisfy these criteria are called open zones.
The two types of zones are merely a convenient way to break up
the interval for clustering. Both kinds of zones can provide meaningful
dips, depending on the quality of the correlations.
Zoning
is a preliminary sorting procedure. Both stable and open zones
are subsequently treated in the same fashion. Zone length can
vary from one to fourteen consecutive displacements. No indication
of the zoning used is shown in the output arrow plots or the standard
output listing.
The
correlation coefficient measured along with the displacement correlation
is an important criterion of the quality and is not ignored in
the choice of good correlations. To account for this, the dip
points placed on the scattergram are weighted according to a coefficient
called the level weight. A greater weight raises the contribution
of retained dip determinations and enhances their chances of being
selected as candidates for clustering.
If
the quality of the correlation reported for the level by the source
dipmeter program is good, the contribution to the level weight
is 3, if fair, it is 2, if poor, it is 1. If the level shows four
arm closure (a double asterisk on the original listing), weighting
is doubled. Thus, the level weight varies from 1 (poor) to 6 (excellent).
Clusters
thus identify the probable ranges of dips for the zone. The program
returns to each dip level in turn and retains only those dip determinations
which fall within one of the clusters. If one is found in the
highest ranked cluster, it is retained, and if there are two or
more, their vector average is retained. If none are found, the
program can expand the area included in the cluster. If cluster
expansion fails, the cluster of next lower rank is checked.
It
may happen that no contribution is found from a level to any of
the defined clusters, in which case this level is considered to
have no result. Similarly, if no clusters are found at all within
the zone, no result is shown on the output listing. This occurs
when the data are so poor that no meaningful displacement combinations
can be made.
Since
clustering only uses data from a previously applied dipmeter program,
it cannot find new correlations and it cannot find dips where
none were found on the original. It may be possible to obtain
new results in "no result" intervals by reprocessing
the original dipmeter with new parameters.
A
typical set of input data to CLUSTER is shown below, followed by output for the same interval.
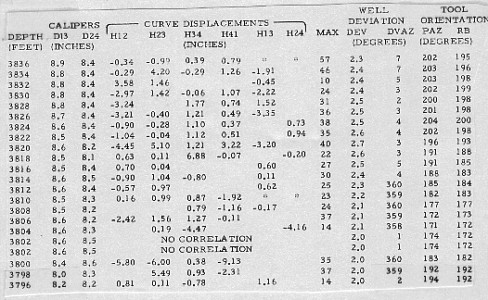
Input data to dip clustering program
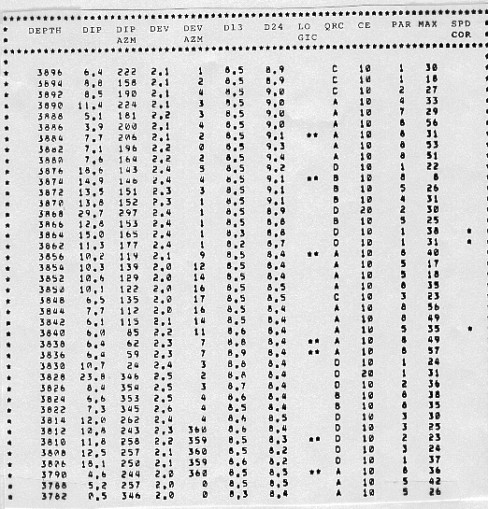
Output data from dip clustering program
The
process of dip retrieval that has just been described systematically
attempts to provide one dip for each correlation window. However,
the basic idea of the method is that consecutive correlation intervals
must overlap, in order that dominant anomalies can affect the
clustering process. As a result, it is quite usual that the same
dip is repeated twice when the overlap between consecutive levels
is 50 percent of the correlation length, or four times when the
overlap is 75 percent.
Users
of dipmeter surveys should train themselves to recognize doublets
or quadruplets as representing a single anomaly. However, it would
be nice if the computer would do the same and represent it by
a single dip result, at the midpoint between the depths of the
two or four component levels. This is accomplished by pooling
clustered dip results.
Pooling
consists of testing the results from successive levels, up to
a number of levels called the pooling constant and controlling
whether their angular dispersion does not exceed a fixed value,
called the pooling angle. If the test is satisfied, the component
dips are replaced by their vector sum, the pooled vector. Its
dip magnitude and azimuth are converted to geographic coordinates
and printed out at the mean depth, together with other data about
the computation. The sample below can be compared to
the un-pooled results shown earlier .
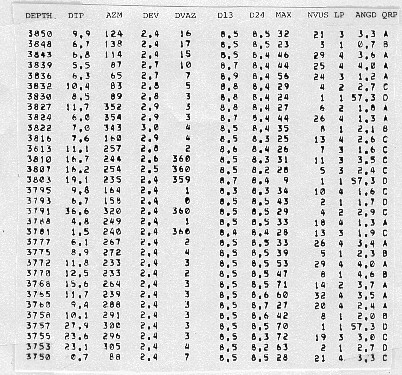
Output data from dip pooling program
Two
separate output files are created: one for the clustered data
and one for clustered and pooled data. Thus, in reality, two different
dipmeters are created from the same data, using different rules
in their analysis.
The
illustration below (left side) shows an arrow plot for clustered and pooled
results. The arrows with black circles represent high quality
ratings. Usually a blackened circle corresponds to pooled results;
however, it is possible that a non-pooled result from a high quality
level could plot as a blackened circle.
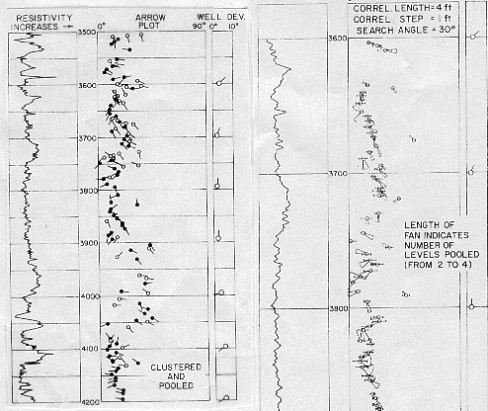
Dip plot of clustered and pooled data (left),
dip fan or range plot (right)
Pooled
results are generally plotted on 1 or 2 inch per 100 feet depth
scale. This can be done since there are fewer arrows to plot.
Thus, one use of pooling is to provide a dip record on a depth
scale commonly used for correlation. Usually, structural analysis
is all that can be accomplished with this plot.
The
arrow plot represents dip magnitude and azimuth from the output
listing at their proper depth. However, it does not represent
the effect of uncertainties, as represented by the dispersion
of dip values and their directions in the original data. The fan
plot is a method to present this knowledge as the quality indicator
instead of the more usual open or filled circles. A sample is
shown below (right).
In
the fan plot presentation, a small circle surrounds the center
value of dip magnitude. A small line segment extends on both sides
from a lower to a higher dip magnitude value, essentially indicating
an error bar. In similar fashion, a fan extends from a lower to
a higher dip azimuth value. These values are determined from the
combination of the pooled dip magnitudes and azimuths and the
angular dispersion parameters. They encompass all values within
one standard deviation from the mean. The length of the fan represents
the number of dips used in the statistic. Thus, it is probable
that the true dip is contained inside the possible values within
the fan, both in magnitude and azimuth.
The
same value of the angular dispersion parameter may correspond
to a nearly closed fan at high values of dip to a wide open fan
near zero dip magnitude. When angular dispersion exceeds dip magnitude,
the azimuth value cannot be specified with any kind of certainty
and no fan is drawn.
|

