|
 Pattern Recognition For
Dip
Calculations
Pattern Recognition For
Dip
Calculations
In 1977, Schlumberger developed a dipmeter program that used pattern
recognition instead of cross correlation to find dip angle and
direction. The aim of the program, called GEODIP, was to reproduce,
as much as possible, the ability of the human eye to recognize
and match similar details on curves which are usually, but not
necessarily, nearly identical. Dresser Atlas offers a program
called STRATADIP which is similar in concept to GEODIP. The
general concepts are still used today in modern dipmeter and
resistivity microscanner dip calculations.
The
following description was paraphrased from “An Approach
to Detailed Dip Determination Using Correlation by Pattern Recognition”,
P. Vincent et al, SPE Paper 6823, 1977.
One
of the objectives of GEODIP is to overcome the rigidity of the
fixed correlation interval procedure and provide a density of
information more closely related to the geological detail seen
on cores. There was also the feeling that the dipmeter raw data
contained more information than was actually being used, even
by the improved processing achieved with clustering and pooling.
After all, the electrodes had a resolution of 0.2 inches and often
one or two foot data was being presented.
Many
features, such as peaks and valleys, are identifiable by eye from
curve to curve on the dipmeter. These features have various thicknesses
(from one inch to several feet), amplitudes, and shapes. Each
feature may be considered to be the signature of a geological
event in the depositional sequence. Moreover, the dip of the bedding
is not necessarily constant, and may sometimes vary rapidly. The
method of correlation by pattern recognition is best adapted to
automatically detect these curve features, to recognize them from
curve to curve, and to derive dips for the boundaries of each
individual feature.
Different
curve features of the same type are often very similar and easy
to confuse. The human correlator avoids this ambiguity by constant
eye movements to confirm or invalidate hypothetical correlations.
In so doing, the correlator implicitly, often unconsciously, applies
some logic rules which are integrated into the perception process.
In the GEODIP method, equivalents of such rules and safeguards
are included, as far as they have been recognized, in the program
logic. Programs of this type have been called expert systems,
or knowledge based systems, because they contain the rules of
experienced analysts.
The
method is constructed around a basic law justified by geological
conditions of deposition, the rule of non-crossing correlations.
This rule states that the layers are deposited one over another,
so that they can wedge out but they cannot cross. The consequence
is that if Event A appears above Event B on one curve, it cannot
appear below B on another one. This rule induces a certain interdependence
between all of the correlations. In this method, the correlations
are not viewed as independent realities, but as parts of a more
general structure having internal organization and rules.
Where only two curves are considered, it is a simple matter to
recognize crossover correlations and disregard them. But when
more than two curves are involved complex logic is
required within the computer program to perceive that the correlation
(A1, A2), is inconsistent with the correlations (B1, B3) and (C2,
C3). Actually, it is the set of the three correlations which is,
as a whole, inconsistent. It cannot be inferred, from what is
shown, which one is incorrect.
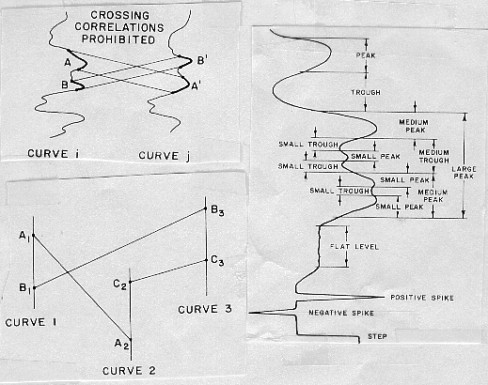
Dip curve pattern recognition definitions
The
goal of the computer logic is to select the largest set of curve
to curve correlations that does not include any crossovers or
implied crossovers. To meet this goal, a branch of modern mathematics
called the theory of partially ordered sets has been applied to
the description and consistency checking of sets of correlations
between curves. While this theory is necessary to properly implement
on a computer the rule of non-crossing correlations, an understanding
of the mathematics is not needed to appreciate what it achieves.
The
method of correlation by pattern recognition is composed of two
main phases:
1. feature extraction (detection of curve elements)
2. correlation between similar features
In
phase one, each curve is analyzed individually with reference
to a catalog of standard patterns or types of curve elements,
such as peaks, troughs, spikes, and steps, and is decomposed into
a sequence of such elements. At the end of the feature extraction
phase, the curves are replaced by their description in terms of
elements.
Each
element is associated with one or two boundaries which give the
position of the element on the initial curve as well as a pattern
vector, which is a series of numbers characterizing the shape
of the element. The pattern vector for a peak contains a description
of its:
1. average (P1)
2. maximum (P2)
3. position of maximum, Xm, relative to boundaries, B1 and B2,
given by P3 = (Xm - X1) / (X2 - X1)
4. maximum minus average (P4)
5. balance left/right inflection point smoothed derivative values
(d1 and d2),
given by P5 = -(d1 /d2) / (1 + d1 / d2)
6. left jump (P6)
7. right jump (P7)
8. balance left/right jump,
given by P8 = -(P6 / P7) / (1 + P6 / P7)
9. width of peak (P9)
Other
features have their own unique list of parameters in their pattern
vector.
In
the correlation phase, the method tries to successively match
elements of one curve to similar elements of the others. The objective
is to recognize the same geological event as it appears on different
curves. The basic criterion is the comparison of pattern vectors.
To find these correlations, a coefficient is computed which is
a measurement of the likeness between any two elements, using
the following equation:
1: L = SUM ((Pai - Pbi)^2)
Where:
L = likeness coefficient
Pai = ith parameter for an element in curve A
Pbi = ith parameter for a similar type element in curve B
Low
values for L mean a high degree of likeness.
Then,
the procedure attempts successive correlations according to a
built in order of precedence: large troughs, then large peaks,
then medium troughs,...
The
program retains already accepted higher precedence correlations
in order to forbid crossing them in further attempts with correlations
of lower rank.
When
two elements are considered to be a match, the corresponding upper
and/or lower boundaries are then correlated. The resulting dips
are computed from the displacements measured between these correlated
boundaries and not those measured between the elements themselves.
At
the beginning of the correlation phase, an initial search angle,
corresponding usually to the highest value of expected dip magnitude,
is imposed. The initial search distance is computed from the input
search angle, the orientation parameters, and the diameters measured
by the tool at the particular level. As correlations are made
and accepted, the search distances are modified, as necessary,
to avoid crossing correlations.
It
may happen that no large element can be correlated with any large
element of the same type on the search curve. To handle these
cases in following passes, requirements are relaxed, for instance,
by authorizing the correlation of a large element of the base
curve with a medium element of the same type on the search curve.
On the other hand, the correlation of unlike elements, such as
peaks with troughs, is forbidden.
Thus,
the correlation phase proceeds by successive passes, searching
first for the most obvious correlations, those having the lowest
likeness coefficients. Each time a correlation is retained, it
is memorized in order to limit subsequent search lengths for correlations
with higher likeness coefficients.
Pattern
recognition correlation is also used in determining the velocity
correction, allowing almost inch-by-inch detection of speed variations.
The
image below shows the graphic presentation made by automatic plotter.
Because of the large number of dip results found, a depth scale
of 1/40 (30 in. per 100 ft.) or 1/24 (50 in. per 100 ft.) is used
instead of the usual 1/240 or 1/200 scales. This uncommon depth
scale is better adapted for the high resolution available for
very thin beds. The semi-horizontal lines connecting the traces
represent the correlation of element boundaries.
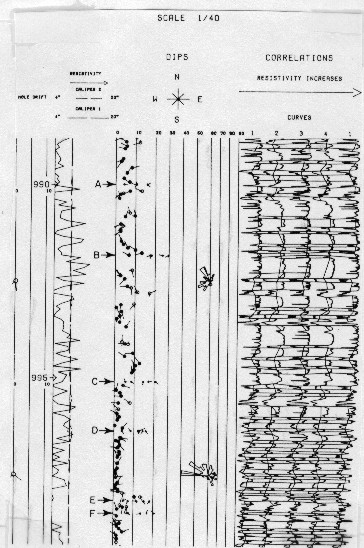
Output plot for pattern recognition dip program GEODIP
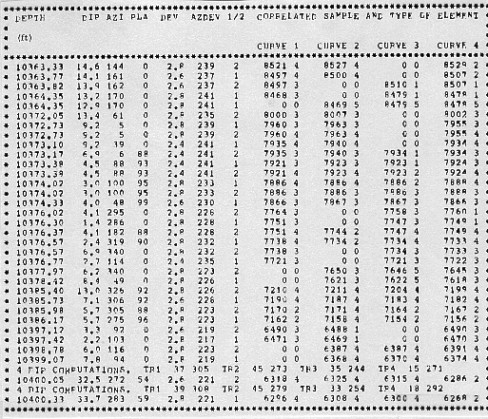
Output listing for pattern recognition dip program GEODIP
With
GEODIP there is no quality rating of the dip determination. The
visual display of the curves and the correlations enable analysts
to decide for themselves about the reliability of the correlations
according to the character of the curves. Comparison to core data
is one way to check the validity of the results of stratigraphic
analysis.
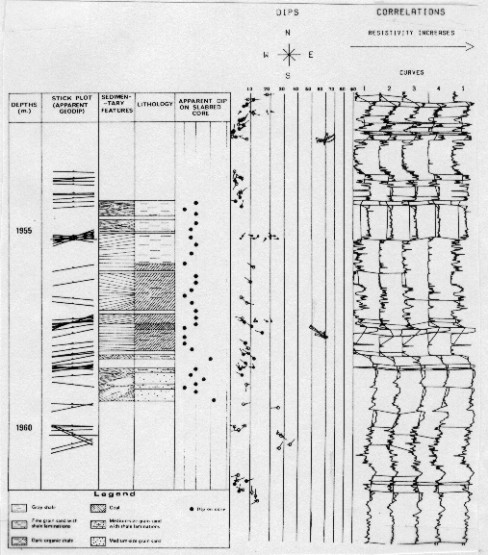
Core comparison to pattern recognition dip program GEODIP
|

