|
 Stratigraphic
High Resolution Dip Calculations
Stratigraphic
High Resolution Dip Calculations
This
Section describes the current mathematical approaches to dip
calculations from a multiplicity of dip curves. The method
now in vogue
combines both structural information as in pooled clusters and
stratigraphic correlations as in GEODIP.
The SHDT and its companion computation program, DUALDIP provides
this, with three independent computations of formation dip.
These methods are currently in use for resistivity
microscanner and acoustic televiewer dip calculations.
This
3 pronged approach allows the possibility of adapting the interpretation to the specific
problem of interest, whether structural, sedimentary, or sand
body geometry. SHDT and DUALDIP are Schlumberger trademarks. The
three calculation modes described below were extracted from “Applications
of the SHDT Stratigraphic High Resolution Dipmeter”, Yves
Chauvel et al, Trans SPWLA, 1984.
 MSD Dips (Mean Squares)
MSD Dips (Mean Squares)
These result from all the possible cross correlations between
couples of sensors, giving up to 28 curve displacements at each
level. The correlations are done in the standard way, and require
definition of correlation length, step distance, and search angle.
A plane is then fitted through all the available results, using
a repetitive logic of discarding the most distant displacements
and then refitting. This results in either:
- a good quality dip (full arrowhead) if distances from mean are
small and few displacements are discarded.
- a low quality dip (open arrowhead) or no dip at all, if distances
from mean are large and/or many displacements are discarded.
There
is no vertical continuity logic or clustering routine in the MSD
computation, and each level is autonomously processed. The clustering
is thus replaced by an analysis of the local scattering of the
displacements. This method benefits from the ample redundancy
available from 28 displacements, while two would be enough to
define a dip, reducing the possibility of producing random dips
or noise correlations.
 CSB Dips (Continuous Side-by-Side)
CSB Dips (Continuous Side-by-Side)
While the MSD dips respond to major geological events, the CSB
focuses on fine details very much like a geologist studies the
sedimentation of a sequence through the inspection of a core.
Each pair of twin curves (eg. electrodes 1 and 1A) is cross correlated
on a fine interval (typically, 12" x 3"). This gives
a vector parallel to the dip plane. Another vector is found at
the same depth by cross correlation of an adjacent pair of twin
curves (eg. 2-2A). Taken together, the two vectors define a dip
plane. The CSB dips will be as dense as the step length chosen
permits (eg. up to 4 per foot for a 12" x 3" computation).
With
only four side-by-side correlations, the only cross check available
is to verify that, for a planar bed, the displacements obtained
from opposite pairs of curves (eg. 1-1A and 3-3A) should be equal
in value and opposite in sign. This occurs if closure error is
zero. If this is the case, any combination of these displacements
yields the same dip and any orthogonal pair is used to produce
the dip at that depth. If this is not the case, a window is opened
around the level under examination, and the vertical continuity
of the displacements within the window is checked. The orthogonal
pair showing the smoothest continuity within the window is selected
for dip computation.
Whether
a good quality dip (full arrowhead), a low quality dip (open arrowhead),
or no dip is output, is a function of the quality of the side-by-side
correlations established and of the vertical continuity of the
displacements.
 LOC Dips (Local Derivative)
LOC Dips (Local Derivative)
An event detection logic is used on the eight curves to establish
pinpoint correlations between events on the curves. As in GEODIP,
the computer processing uses a derivative filter to obtain absolute
dips independent of dips at other depths, similar to what could
be found by manual correlation. There are however a few differences.
To
be retained as a LOC dip, an event has to be recognized on at
least 7 of the 8 curves, while the GEODIP logic requires only
3 out of the 4 curves. Thus the LOC dip logic is more demanding
than the GEODIP logic, which explains why generally fewer LOC
dips are obtained than GEODIP results on comparison runs.
The
LOC dips are further refined by a cross correlation made on a
12" interval, while GEODIP results are computed directly
from the spot events on the curves. This cross correlation involves
the eight curves and includes a repetitive best fit and rejection
logic as in the MSD computation, with similar criteria for quality
coding (full or open arrowhead).
A
measurement of the planarity is derived from each of the possible
dip planes at any level. The retained value corresponds to the
surface which best approximates the set of these planes. By convention,
a perfectly planar surface has a planarity of 100.
Some
events are recognized on only some of the dip curves. In this
case, the available correlations are traced across the applicable
curves, with an optional notation of "F" (Fracture)
or of "P/L" (Pebble/Lens) for single pad events or two/three
pad events, respectively. These interpretations, however, are
not to be considered as certain, but rather as possible.
Due
to their origin (pad-to-pad correlations), the LOC dips have meaningful
lateral significance. If structural dip is present, it will normally
be seen by the LOC dips rather than by the CSB dips. Generally
the statistical agreement between the LOC and the MSD dips can
be expected to be quite good.
DUALDIP
is the computer program which produces the standard SHDT result
presentation. This includes CSB and LOC dips, the eight dip curves,
the synthetic resistivity and gamma ray curves, calipers and hole
drift data. The depth scale is usually 1/40, and as an option
the MSD dips can be added to this output. A sample is shown
below.
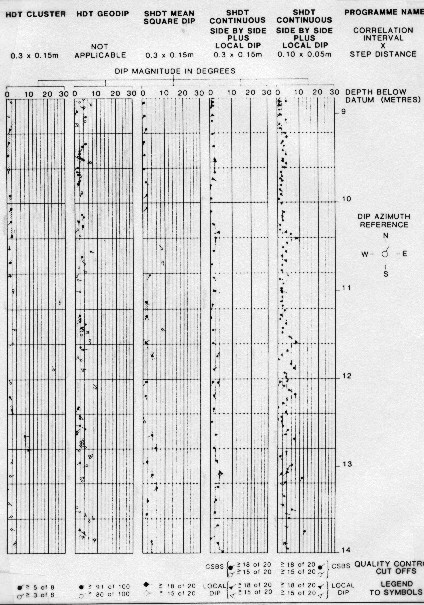
MSD, CSB, and LOC dips from SHDT dipmeter
Structural
interpretation is done using the MSD dips. Due to the logic used,
namely cross correlation made using long intervals, the MSD dips
are the ones likely to represent laterally significant and vertically
consistent geological events. For optimum use of the MSD dips,
a reduced scale (1/200) plot is normally produced. This plot is
also the single SHDT product when no fine scale studies are contemplated.
The
prime objective of the SHDT tool design is to improve the ability
to provide reliable answers to sedimentary interpretation problems.
While the rules of interpretation remain essentially the same
as in HDT interpretation, there are additional possibilities.
Among the information that can be retrieved by visual analysis
of the dip curves, reconstructed resistivity, and dip arrows are:
-
type of lithology (shale, sand, conglomerate) from the shape and
likeness of the curves.
-
fining upwards, coarsening upwards sequences. This is done by
analyzing the resistivity variations across the sequence, either
with the dip curves themselves or with the synthetic resistivity
curve. Other open hole logs, such as the gamma ray (combinable
with SHDT), are useful here. Care should be exercised using the
resistivity, however, since fluid saturations have to be accounted
for when inferring grain size variations from resistivity gradients.
-
homogeneous bodies (no apparent bedding) as opposed to finely
striated, laminated bodies.
-
parallel vs nonparallel bedding. This is especially important
in sandstones, and has found recent applications to the study
of turbidites.
-
correlation lines: some correlations involve the eight resistivity
curves, some do not. The most appropriate interpretation (pebble,
lens, fracture, other) will be made on the basis of the dip curves
(conductive or resistive anomaly, number of pads involved, etc.).
-
fractures: open fractures will show as isolated conductive spikes
which may or may not correlate with similar spikes on other dip
curves.
Some
of the important uses of the CSB dips are:
- determination of bedding angle and direction in those (frequent)
cases where they do not show as MSD (or LOC) dips. This is the
case, for example, in coarse grained sandstones where bedding
is only indicated by minute changes of resistivity, and not by
the existence of large contrasts. This is also very common in evaporitic sequences.
-
determination of the direction of sediment transport, a corollary
to the above. This is especially interesting in severe cases of
cross bedding, when the only dips produced by long interval correlations
generally correspond to those of the individual sedimentary units,
seen at their interfaces, and not to the actual current bedding
surfaces.
-
conventional sedimentary interpretation (red, blue patterns, direction
of sand body thickening, etc.). All of this can be done on an
almost microscopic scale.
CSB
dips are also very useful, and often better than MSD dips, in
high angle apparent dips, when longer correlation intervals are
used.
LOC
dips can be used to study such features as:
-
nonparallel bedding, for example, when the upper and the lower
boundaries of thin beds do not have the same dip. In cases of
poor planarity, the event recognition logic will be too tight
for a LOC dip to be produced, and the MSD curves may then provide
the answer. This is particularly important if this bed is to be
found in another well, or when looking for the direction of updip
or downdip thickening.
-
cross bedding: the LOC dips will see the interfaces between the
individual sedimentary units, when apparent. This dip may not
coincide with the angle and direction of deposition in cross bedded
formations (eg. tabular bedding, foreset beds).
-
turbulence of deposition, when causing non-planarity of bedding.
The
MSD dips are normally not used for sedimentary studies, being
the result of an averaging of the dip curve anomalies over the
length of the correlation interval. They are usually presented
on the DUALDIP plots, however, for structural reference. The vertical
(depth) scale used for stratigraphic work makes it difficult to
see structural patterns in the MSD data.
|

