|
 Reservoir Quality from Net Reservoir
Reservoir Quality from Net Reservoir
There are a number of ways to assess reservoir quality. In laminated
sands, one approach is to correlate first three months or first
year production with net reservoir properties from the laminated
models described above. We chose to use the first 8760 hours of
production (365 days at 24 hours each) divided by 4 (3 months
of continuous production) as our “actual” production
figure. This normalizes the effects of testing and remedial activities
that might interrupt normal production.
The normalized initial production was correlated with net reservoir
thickness, pore volume (PV), hydrocarbon pore volume (HPV), and
flow capacity (KH) from the laminated Model C. Correlation coefficients
(R-squared) are 0.852, 0.876, 0.903, and 0.906 respectively. The
correlation is made using data calculated over the total perforated
interval. The other three analysis models did not give useful
correlations nor did model C when only a single shale indicator
was used. Results of the correlations are shown below.
Average
shale volume was correlated with actual production but the correlation
coefficient was only 0.296, although the trend of the data is
quite clear.
 Reservoir Quality from an Enhanced Shale Indicator Reservoir Quality from an Enhanced Shale Indicator
Another approach is to calculate a quality curve:
1. Qual2 = RSH * GR / RESD
This
amplifies the shale indicator in cleaner zones and is scaled the
same as the GR curve. A net reservoir cutoff of Qual2 <= 50
on this curve was a rough indicator of first three months production,
but the correlation coefficient was as poor as for average shale
volume. QUAL2 does make a useful curve on a depth plot as it shows
the best places to perforate when density and neutron data are
missing.
 Reservoir Quality from Hester’s Number Reservoir Quality from Hester’s Number
Another quality indicator was proposed by Hester (1999). It
related neutron-density porosity separation and gamma ray
response to production, based on the graph shown below..
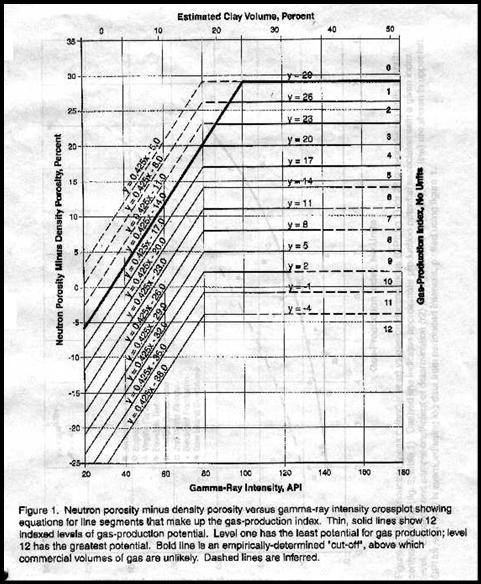
Hester’s reservoir quality indicator (QUAL1)
This
graph is converted to a numerical quality indicator (Qual1) in
a complex series of equations that represents predicted flow rate.
The
equations, as displayed in the Lotus 1-2-3 spreadsheet are as
follows:
1:
ND_DN = 100 * (PHIN - PHID)
2: E = @IF(ND_DN>(0.425*GR)-14,0,@IF(ND_DN>(0.425*GR)-17,4,
@IF(ND_DN>(0.425*GR)-20,5,@IF(ND_DN>(0.425*GR)-23,6,
@IF(ND_DN>(0.425*GR)-26,7,@IF(ND_DN>(0.425*GR)-29,8,
@IF(ND_DN>(0.425*GR)-32,9,@IF(ND-DN>(0.425*GR)-35,10,11))))))))
3: F = @IF(ND_DN>(0.425*GR)-35,0,@IF(ND_DN>(0.425*GR)-38,11,12))
4: G = @IF(ND_DN>(0.425*GR)-14,0,@IF(ND_DN>29,0,@IF(ND_DN>26,1,@IF(ND_DN>23,2,@IF(ND_DN>20,3,
@IF(ND_DN>17,4,@IF(ND_DN>14,5,0)))))))
5: H = @IF(ND_DN>14,0,@IF(ND_DN>11,6,@IF(ND_DN>8,7,@IF(ND_DN>5,8,
@IF(ND_DN>2,9,@IF(ND_DN>-1,10,@IF(ND_DN>-4,11,12)))))))
6: I = @IF(E=0,F,E)
7: J = @IF(G=0,H,G)
8: QUAL1 = @IF(GR<80,I,J)
Where:
ND_DN = neutron minus density porosity difference in sandstone
units (percent)
PHID = density porosity sandstone units (fractional)
PHIN = neutron porosity sandstone units (fractional)
GR = gamma ray (API units)
QUAL1 = Hester Quality Number (unitless)
E, F, G, H, I, J = intermediate terms
Note
that these nested IF statements are slightly different than those
originally published by Hester. The changes correct for typographical
errors in the original paper.
There
is a flaw in Hester’s paper that can be cured. He does not
account for zone thickness or attempt to find a net reservoir
number. He uses only the average quality number over the zone,
which presupposes that all perforated intervals are equal in thickness.
To overcome this, we can use a quality cutoff and obtain a thickness
weighted quality and correlate this to actual production.
A
Hester quality of 4.0 or higher reflects reservoir rock that is
worth perforating, and gives similar net reservoir thickness as
the previous indicators. Graphs showing the correlation of actual
production to net reservoir with QUAL1 >=5 and >=4 are shown
below. The regression coefficients are 0.856 and 0.837
respectively. Although this looks pretty good, the low rate data
is clustered very badly and other indicators work better in low
rate wells.
The
Hester quality number QUAL1, along with QUAL2 = GR / RESD, are
the only quality indicators that show where to perforate. The
other indicators described here give a reasonable estimate of
reservoir performance, but do not give any indication of how to
economically complete the well.
 Reservoir Quality from Productivity Estimates Reservoir Quality from Productivity Estimates
A productivity estimate based on a log analysis version of the
productivity equation has also proven useful The equation used was:
1. ProdEst = 6.1*10E-6 * KH * ((PF - PS)^2) / (TF + 273) * FR
* 90
The
leading constant takes into account borehole radius, drainage
radius, viscosity, and units conversions. KH is flow capacity
in md-meters. (PF - PS) is the difference between formation pressure
and surface pressure in KPa. A constant value of 1300 KPa was
assumed for this study. Clearly, more detailed data could be used
if time permits. TF was chosen constant at 20 degrees Celsius.
FR
is a hydraulic fracture multiplier, chosen as 2.0 for this study,
based on the 9 wells used to calibrate to 3-month initial production
data. The constant 90 converts e3m3/day into an estimated 3-month
production for comparison to actual. The 3 month numbers were
chosen instead of daily rate as they have more “heft”
and can be equated to income more readily.
Note that
the equation used is a constant scaling of KH, so the correlation
coefficient is the same as the KH graph at 0.906.
 Case History - Milk River, Alberta
Case History - Milk River, Alberta
The sample depth plot
below shows typical results of
the prototype analysis. The majority of the results are from the
conventional analysis Model A, including the PayFlag. Some of
the input curves are shown in Tracks 1 and 2. Hester’s quality
factor (QUAL1) and the GR/RESD quality factor (QUAL2) are shown
in Track 4. This is a gas producing well with an excellent set
of perforations, shown on the right-hand edge of Track 2.
The
conventional analysis, plotted in Track 5, gives a clear picture
of why the conventional approach is so discouraging. Unfortunately,
the laminated models do not create output curves that are consistent
with a depth plot, so it is impossible to make pretty pictures
of the results except in map form.
In
the current Milk River study, this model appears to be the
most effective in predicting reasonable reservoir properties.
PHIMAX was set at 0.20, based on core data, and KBUCKL was
set at 0.040, based on experience. CPERM and DPERM were
chosen as 18.3 and -3.00 respectively from the core data
crossplot shown earlier.
A
total of 10 reservoir quality indicators for each of 3 reservoir
layers, plus the cored interval and the perforated interval were
generated for each of 4 different analysis models. The best model
for predicting productivity is Model C, using the minimum of 3
shale indicators. The density neutron porosity separation indicator
is essential to the success of Model C.
The
best productivity indicator is the flow capacity (KH) or its equivalent
productivity estimate in e3m3 for 90 days (1st 3 months production
estimate). Five other indicators have strong correlations with
productivity (Net Reservoir, PV, HPV, Hester’s QUAL1 >=5,
and QUAL1 >=4). Hester’s number does not have much resolution
at low flow rates, but clearly separates poor from good wells.
An
important use of the summary tables is to determine whether a
well is under-achieving due to limited perforation interval or
a poor frac job. A comparison of the total KH for the Milk River
compared to the KH for the perforated interval will point out
any problem wells. Even if KH is badly mis-calibrated, the comparison
is useful. Over-achievers may be producing commingled, intentionally
or otherwise, from deeper horizons or may point to log data or
analytical difficulties.
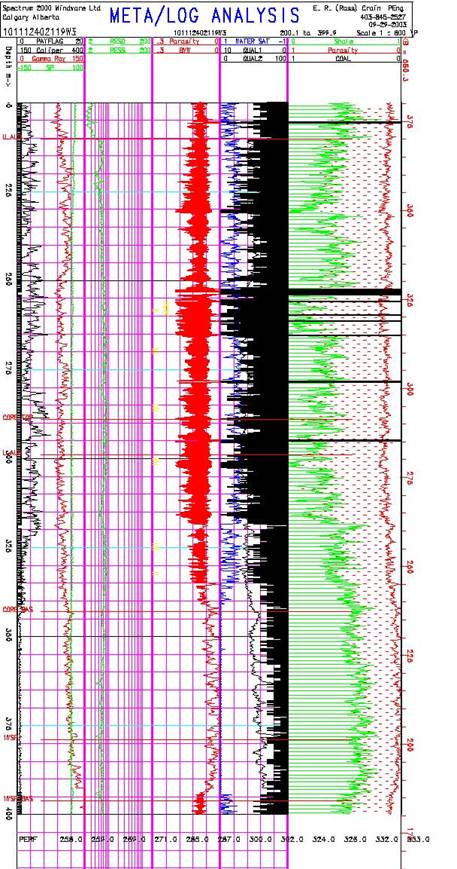
Depth plot showing Hester quality factor in Track
4 (shaded black)
The models can be used to generate a perforation list from Hester’s
quality number or from VSH minimum. An acceptance/rejection filter on the list
will shorten it considerably. This will eliminate intervals that
are too thin to bother with and group intervals that are close
enough to be considered as single intervals.
Because
a full log suite was available in the 9 wells used for calibration,
we have obtained the most likely shale volume (Vsh) result. The
8 wells held in reserve to test the model also showed very good
agreement with initial production. One well that calculated an
IP higher than actual can be brought into line with a small tune-up
of the shale density parameter
for initial production comparison
|

