|
 Lake Maracaibo (Shaly Sand) Lake Maracaibo (Shaly Sand)
This case history is taken from "Quantitative Analysis of
Older Logs For Porosity and Permeability, Lake Maracaibo, Western
Flank Reservoirs, Venezuela" by E. R. (Ross) Crain, P.Eng.
Manuel Garrido, Craig Lamb, P.Geol., Philip Mosher, P.Eng. presented
at GeoCanada 2000, Calgary, AB, May 2000.
During
a project to analyze the log and core data on 150 wells in the
Western Flank Reservoirs offshore in Lake Maracaibo, we developed
a technique to determine accurate values of porosity, water saturation,
and permeability from old ES logs. The depositional environment
is a complicated sequence of superimposed fluvial channels, resulting
in many isolated channels that were not fully drained by nearby
wells. It was therefore necessary to obtain a quantitative reservoir
description for all wells in the project area, even if the log
suite did not lend itself to direct calculation with traditional
log analysis methods.
These
highly detailed reservoir properties from log analysis were augmented
by similarly detailed seismic and stratigraphic correlations,
and integrated together in a reservoir simulator to provide an
accurate historical and predictive model for production optimization.
We would not have been able to do this to a useable level if only
the wells with full porosity log suites were used.
The
method used requires calibration to conventional and special core
data and/or modern porosity log suites. Conventional core analysis
data, electrical properties, and capillary pressure data was provided
in paper form. This data was entered into a spreadsheet database
for processing and was placed in each well file for depth plotting
with the log data. Core data was depth shifted to match well log
depths.
Our
objective was to define a method that would utilize all available
log and core data while providing the most consistent results
between old and new well log suites. A detailed foot-by-foot analysis
was required to allow summations of reservoir properties over
each of many stratigraphic horizons.
Shale
volume (Vsh) was calculated from the gamma ray (GR), spontaneous
potential (SP), and deep resistivity (RESD) responses. The minimum
of these three values at each level was selected as the final
value for shale volume. A unique clean sand and pure shale value
for GR, SP, and RESD were chosen for each zone in each well. A
linear relationship was applied to the Vsh from GR. The resistivity
equation for Vsh is similar to the GR equation, but uses the logarithm
of resistivity in each variable.
Where
a full suite of porosity logs was available, effective porosity
(PHIe) was based on a shale corrected complex lithology model
using PEF, density, and neutron data. The method is quite reliable
in a wide variety of rock types. No matrix parameters are needed
by this model unless light hydrocarbons are present. Shale corrected
density and neutron data are used as input to the model. Results
depend on shale volume and the density and neutron shale properties
selected for the calculation. Therefore, the porosity from this
stage is compared to core porosity where possible, and parameters
are revised until a satisfactory match is obtained.
In
wells with an incomplete suite of porosity logs, we used a model
based on the shale corrected density log, shale corrected neutron
log, or the shale corrected sonic log. Again, a comparison with
core or nearby offset wells with a full log suite is necessary
to confirm shale and matrix parameters.
In
wells without any porosity logs, porosity was based on the shale
corrected total porosity model, where total porosity (PHIMAX)
was derived from offset wells with porosity logs or from nearby
core analysis. The equation used was PHIe = PHIMAX * (1 - Vsh).
This step was the most important contribution to the project as
it integrates all available data in all wells in a consistent
manner.
The
value for PHIMAX was derived from a map of the average of the
total porosity of very clean sands in modern or cored wells. The
map was inspected and a transform created which varied the PHIMAX
value from south to north through the project area. The effectiveness
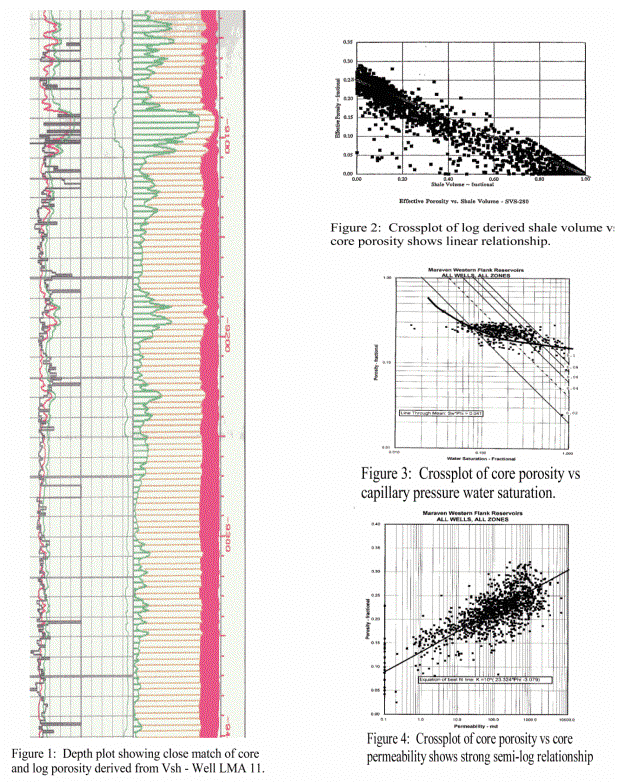
of this method is demonstrated by the close match between core
and log analysis porosity in well LMA 11, shown in Figure 1. Another
way to see this relationship is in a crossplot of log derived
shale volume versus core porosity as in Figure 2.
In
modern wells, PHIMAX is also used to limit the porosity results.
This limit is needed because rough hole conditions or sonic cycle
skips can cause erroneous porosity values to be computed. PHIMAX
is computed as above, but modified by adding 0.03 to the result.
This higher value for PHIMAX prevents the reduction of those few
legitimate porosity results which are slightly higher than usual
on the logs.
From
this stage onward, both old and new wells were treated identically,
with water saturation, permeability, and mappable reservoir properties
being derived in a uniform and consistent manner.
Water
resistivity (RW) was varied with depth to account for the temperature
gradient over the computed interval. These values were confirmed
by the obvious water zones in the lower sands in a number of wells.
Care must be taken to segregate swept zones from original water
zones when checking the RW value. Swept zones show residual oil
on log analysis of between 20 and 60 percent. Back calculation
of RW in a swept zone will lead too high a value for RW.
Water
saturation (Sw) was computed with a shale correction using the
Simandoux equation and with the Waxman-Smits equation. Both equations
reduce to the Archie equation when shale volume is zero. Simandoux
and Waxman-Smits methods gave very similar results in this project
area. The resistivity curves used were the long normal from ES
logs, the deep induction, or the deep laterolog.
The
shale resistivity (RSH) needed for these equations was chosen
by observation of the logs and crossplots. RSH was varied from
well to well to account for differences in response between electrical
logs, induction logs, and laterologs in shale. Resistivity anisotropy
and hole size or mud resistivity effects cause these differences.
The range of values used is small, between 4.0 and 5.0 ohm-m.
Values
of A, M, and N of 1.00, 1.80, and 2.00 were input, based on special
core analysis crossplots. The effect of overburden pressure on
M and N was compared to non-overburden data on the plots where
such data was available. The regression lines for M were pinned
at A = 1.0 because the free regression lines vary too much, due
to the small range in porosity of the core plugs.
Saturation
results were confirmed by comparison to porosity vs capillary
pressure water saturation crossplots derived from the special
core data (Figure 3). When this data is missing in a project area,
it is very difficult to refine the saturation calculation. If
a mismatch does occur, the electrical properties and/or RW and
temperature data must be reviewed and modified if possible, to
obtain a better match to capillary pressure data.
Zones
swept by production from older offset wells are evident on all
newer wells in this project. These zones should not be confused
with the original water zones. Swept zones will produce water
if perforated, but contain 20 to 60 percent residual oil. On raw
logs, the difference in resistivity between a swept zone and an
original water zone may be very small (eg 0.4 vs 0.2 ohm-m in
an extreme case).
An
irreducible water saturation (SWir) was calculated based on a
curve fit to the capillary pressure data, using the following:
IF PHIe > 0.10 THEN SWir = 0.20 / (PHIe - 0.10) ELSE SWir =
1.00. This equation represents a skewed hyperbola through the
porosity vs saturation data in Figure 3.
SWir
was also limited by the Simandoux water saturation such that SWir
could not exceed the Simandoux result. This means that SWir is
the lower of the actual log derived water saturation and the SWir
calculated above. The swept zones are most easily seen on depth
plots by comparing SWir to the Simandoux or Waxman-Smits water
saturation. Where large differences occur, the zone is likely
swept.
Crossplots
of core porosity vs core permeability (Figure 4) gave: Perm =
10 ^ (23.0 * PHIe - 3.00). Detailed crossplots of each zone in
each well, composite plots of each zone for all wells, and a composite
plot of all zones in all wells were made. Differences between
zones and between wells were negligible. Regression analysis to
predict permeability from porosity produces a good average permeability
within a zone. It may not always honour every peak and valley
seen on real cores.
Crossplots
of permeability vs capillary pressure water saturation were also
made. These show a semi-logarithmic straight line relationship.
The plots show that water saturation and permeability are closely
related. High water saturations indicate fine grained, more poorly
sorted, lower permeability, and often shalier zones.
Crossplots
of permeability vs residual oil saturation also show a semi-logarithmic
straight line relationship with higher permeability having lower
residual oil saturations. This is a normal occurrence, and allows
a check of the residual oil saturation seen in swept zones by
log analysis.
Results of analysis on ancient logs, Lake Maracaibo,
Venezuela. Compare core porosity (black curve in left track) with
porosity from PHIMAX (red curve).
On
older wells, previous work used a two step correlation of oil
saturation (So) times porosity (PHI) to the short normal resistivity
(SN) and mud resistivity (RM), of the form:
1.
ln(RT/RM) = A + B * ln(SN/RM)
2. SOPHI = C + D * ln(RT)
This
method was developed by Dr Ovidio Suarez and is documented in
internal reports provided by the client. The parameters A through
D were derived from correlations with hydrocarbon pore volume
(HPV) estimated from core analysis. The method does not account
for borehole effects, invasion, or variations in grain size, sorting,
or shaliness, all of which influence HPV from this type of correlation.
It also does not generate a porosity value, so results cannot
be compared easily to core data and cannot be used to calculate
permeability. Large differences in results between adjacent wells
were noted, leading to the conclusion that these inconsistencies
should be addressed in our new work.
In
the porosity track of Figure 37.17 (above), the green line is
porosity from SOPHI based on the SWe derived in our study: PHIrt
= SOPHI / (1- SWe). This well shows a good agreement between the
two methods but others do not, because the short normal is not
always a good indicator for RT.
It
should be noted, however, that at the time the method was invented,
it was the best approach available for un-cored intervals, since
modern porosity indicating logs had not yet appeared on the scene.
The
results of this study will lead to a significant change in original
oil-in-place compared to the value determined from a strict use
of the prior petrophysical analysis. In addition, all by-passed
pay zones are identified and can become targets for specific in-fill
wells. The reservoir simulation based on this new reservoir description
will have greater predictive power and will be easier to history
match because both reservoir volume and flow capacity are better
defined.
|

